|
1.21
伝達誤差解析ソフトウエア
伝達誤差解析ソフトウエアは, involute
Σ (Spur & Helical)のオプションソフトです. 伝達誤差解析ソフトを使用するためには, FEM歯形応力解析ソフトウエアが必要です.
(1)歯車の回転伝達誤差を解析します.
①歯形誤差, ②隣接ピッチ誤差, ③歯のたわみ, ④軸の振れ, ⑤歯形のすべりの5種類を解析要素として伝達誤差を解析します.
歯車の回転伝達誤差を製品試験するのではなく設計段階で予測することができます.
対象とする歯車は, 2次元歯形応力解析の場合は, 平歯車として解析しますが, 3次元歯形応力解析を使用しますと平歯車とはすば歯車の伝達誤差解析ができます.
図1.45と図1.46に伝達誤差の設定画面を示します.
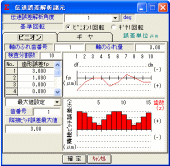 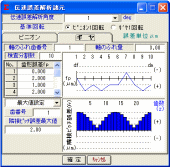
図1.45
伝達誤差設定画面(P) 図1.46 伝達誤差設定画面(G)
(2)伝達誤差の評価1
平歯車の回転伝達誤差グラフを図1.47に,
ワウ・フラッタ(回転変動率)グラフを図1.48に表示します.
また, 周波数より[音]で確認することができます.
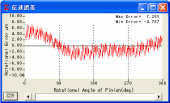 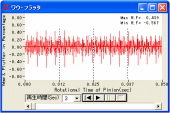
図1.47 回転伝達誤差
図1.48 ワウ・フラッタ
(3)伝達誤差の評価2
図1.49と, 図1.50に, バックラッシを0.1mm, ピニオン軸の振れを10μmとしたはすば歯車の伝達誤差解析とワウ・フラッタの結果を示します. また, 3次元伝達誤差解析は,
かみあい面だけではなく背面干渉も考慮していますのでバックラッシを小さくしたい場合には, 歯のたわみや, 軸の振れを充分考慮して設計する必要がありますが, この3次元伝達誤差解析を使用することにより事前にその限界値を知ることができます.
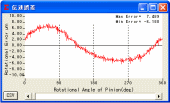 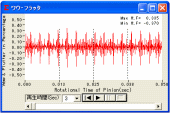
図1.49 伝達誤差(片歯面接触) 図1.50 W&F(片歯面接触)
|
|
1.22
フーリエ解析ソフトウエア
|
平歯車(mn=2,Z1=Z2=40)の回転伝達誤差解析を行い, その周波数解析結果を下記に示します.
ピニオンの歯形は, 図1.51に示すように歯面の中央が凸の状態とし, ピニオン軸に3μmの振れを与え, 1200min-1で回転させたときの回転伝達誤差グラフは図1.52となります.
ただし, ピニオンのピッチ誤差, ギヤの歯形誤差及びギ
ヤの軸振れは無いも
|
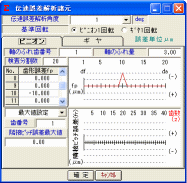
図1.51
伝達誤差設定(P)
|
|
のとします. 周波数解析の結果を図1.53に示しますが, ピッチ誤差等が無いため, かみ合い1次の周波数の800Hz(1200
min-1×40z/60sec), 2次の1600Hz, 3次, 4次の周波数が鮮明に表れています. |
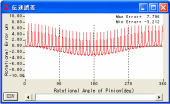 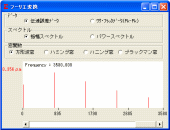
図1.52
回転伝達誤差解析
図1.53
周波数解析
1.23
成形プラスチック歯車の伝達誤差解析
成形プラスチックはすば歯車(POM)を駆動して負荷を与えながら片歯面かみあい試験機で伝達誤差を測定した. 実験に用いた歯車は,
モジュール(mn)1mm, 歯数(Z)37, 圧力角(α)20°ねじれ角(β)20°(右, 左), 歯幅(b)10mmであり, 中心距離(a)を39.47mmとした.
右ねじれ歯車を駆動し, トルクを9.8N・m, 回転数を6min-1として回転伝達誤差を測定した. 測定結果を図1.54に,
その周波数解析結果を図1.55に示す.
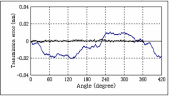 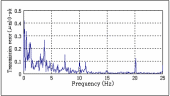
図1.54
伝達誤差試験結果 図1.55
周波数解析
歯形誤差, ピッチ誤差は歯車検査結果に基づいて設定を行い, ピニオン(右)をステップ角1°で回転伝達誤差のシミュレーションを行った結果を図1.56に示す.
その結果, 波形状も回転伝達誤差の最大値も30μmとなりほぼ一致した. また, 図1.57に示すように, かみあい1次の周波数3.7Hzも2次の7.4Hzも顕著に表れている.
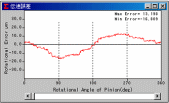 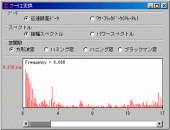
図1.56
回転伝達誤差 図1.57 周波数解析
([1.23]項は, 精密工学会, 2002年講演論文集より抜粋)
|