[付録H] 非対称歯形歯車の特性
H.1 はじめに
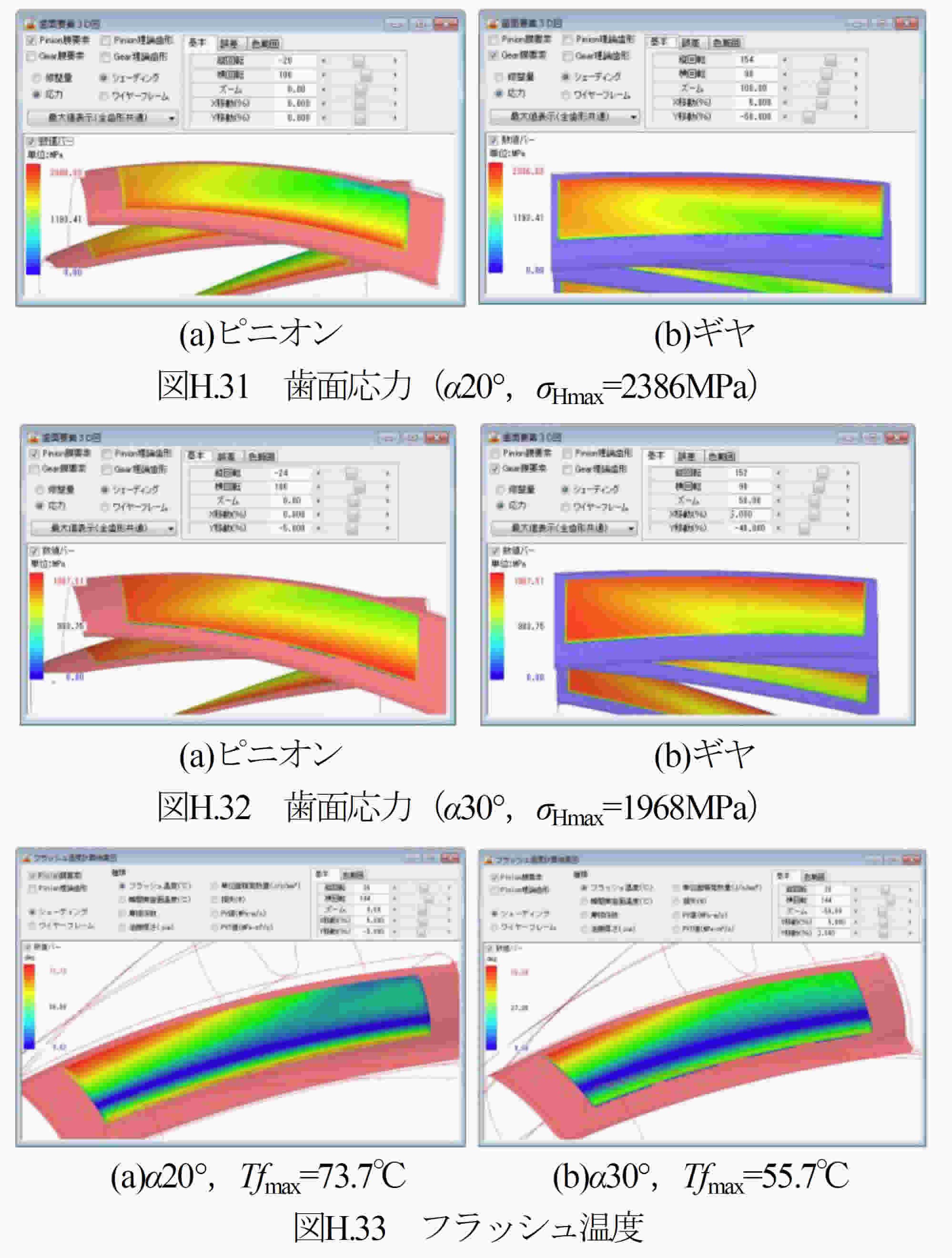
   非対称歯形歯車は，ギヤの大きさや材料を変更しないで負荷容量を増大させることができることから図H.1に示すロシア製 An-70 の contra propeller 駆動の 14000PS ターボプロップの遊星歯車装置に使用されておりAirBus A400Mの1.4倍の能力を有している．また，ヘリコプターのメインドライブギヤにも採用されている1)．このように現在において用途は限定されているが，一般産業機械にも徐々に採用される機運がある．非対称歯形歯車は，創成歯切り加工も研削も可能なことから現在稼働中の歯車装置にも容易に置き換えが可能である．
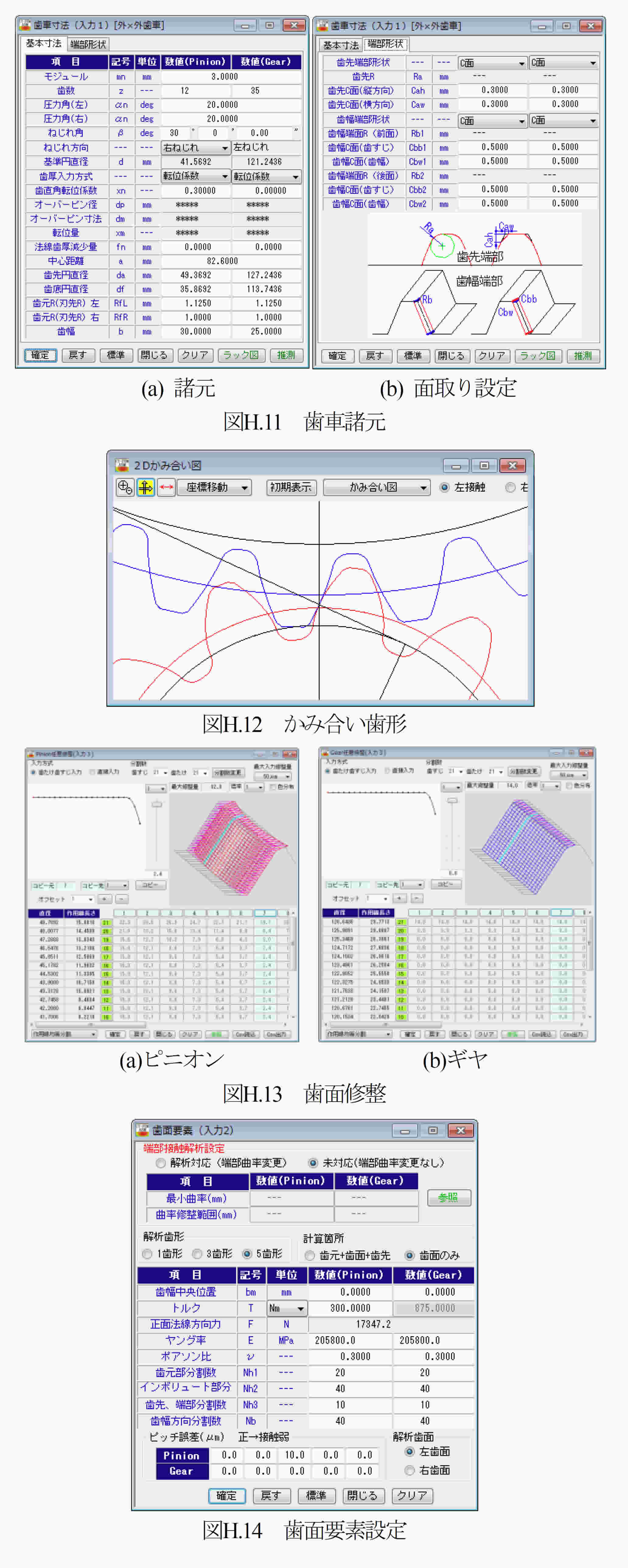
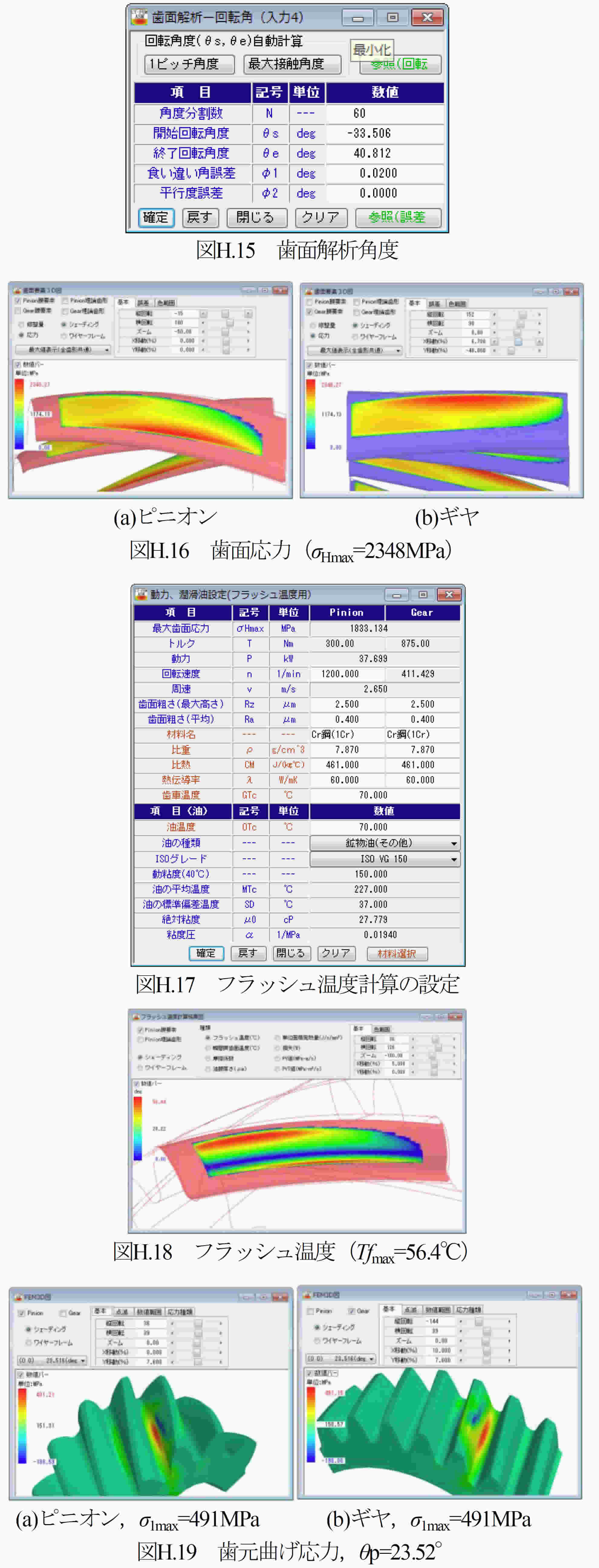
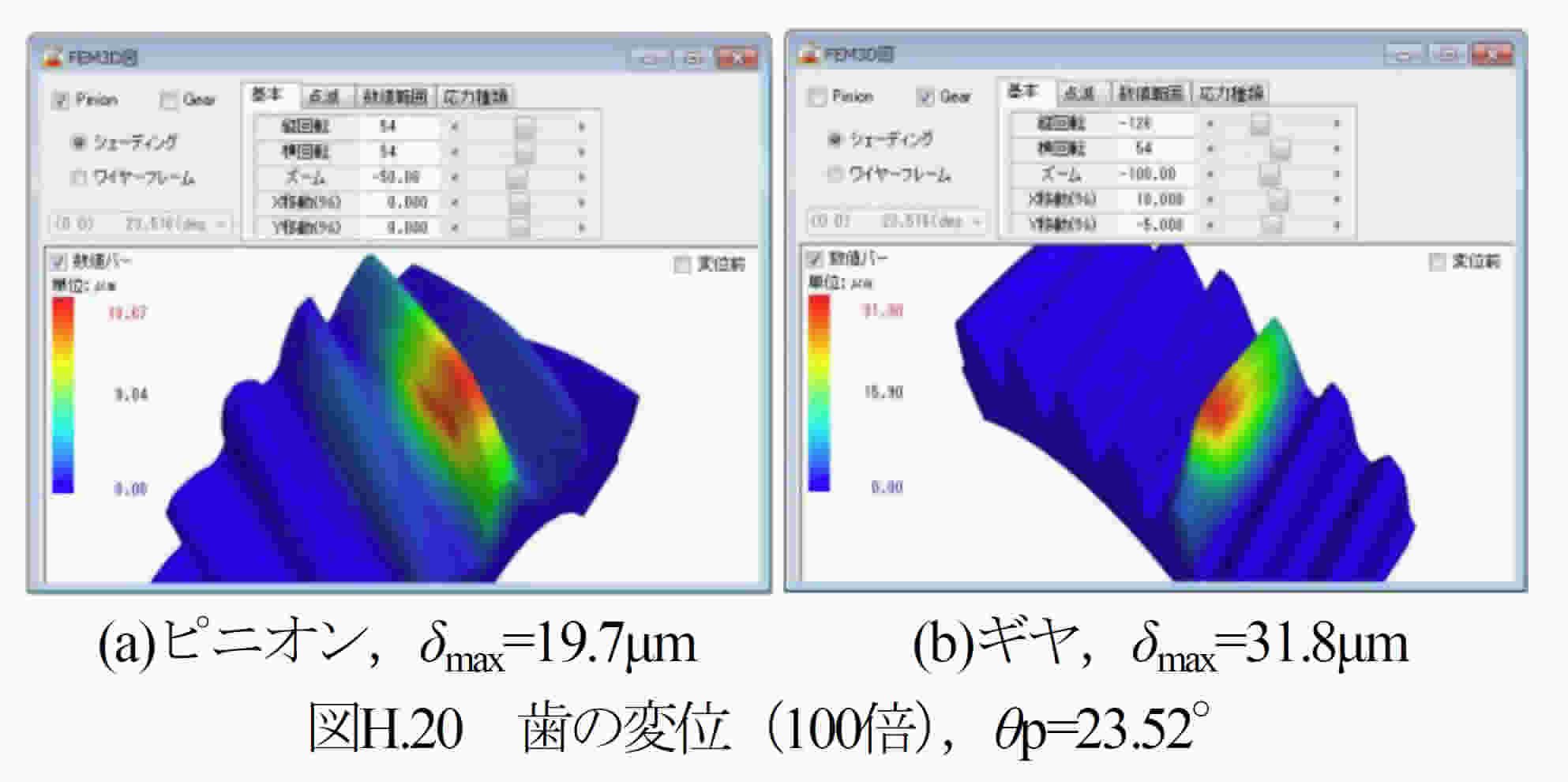
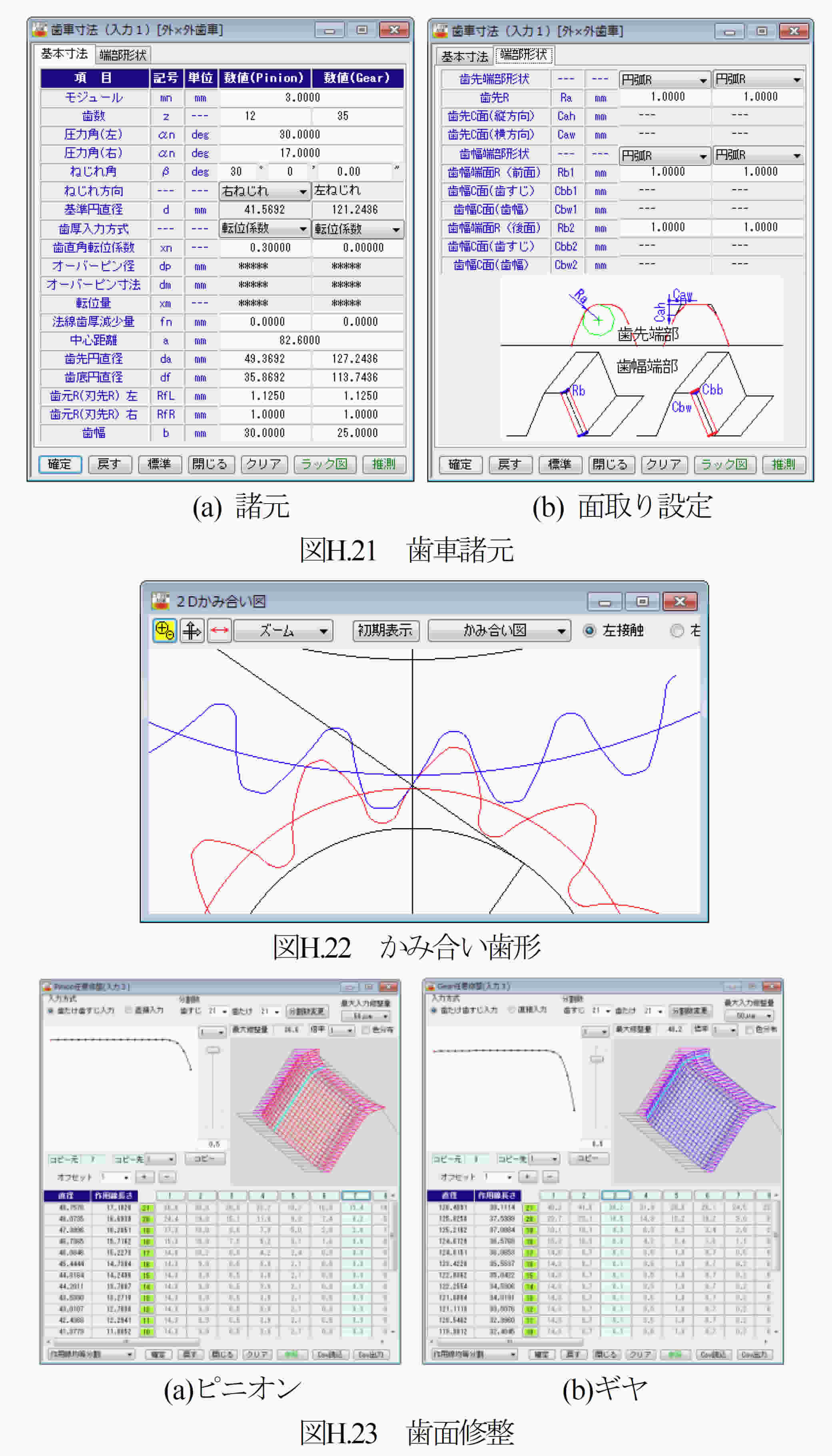
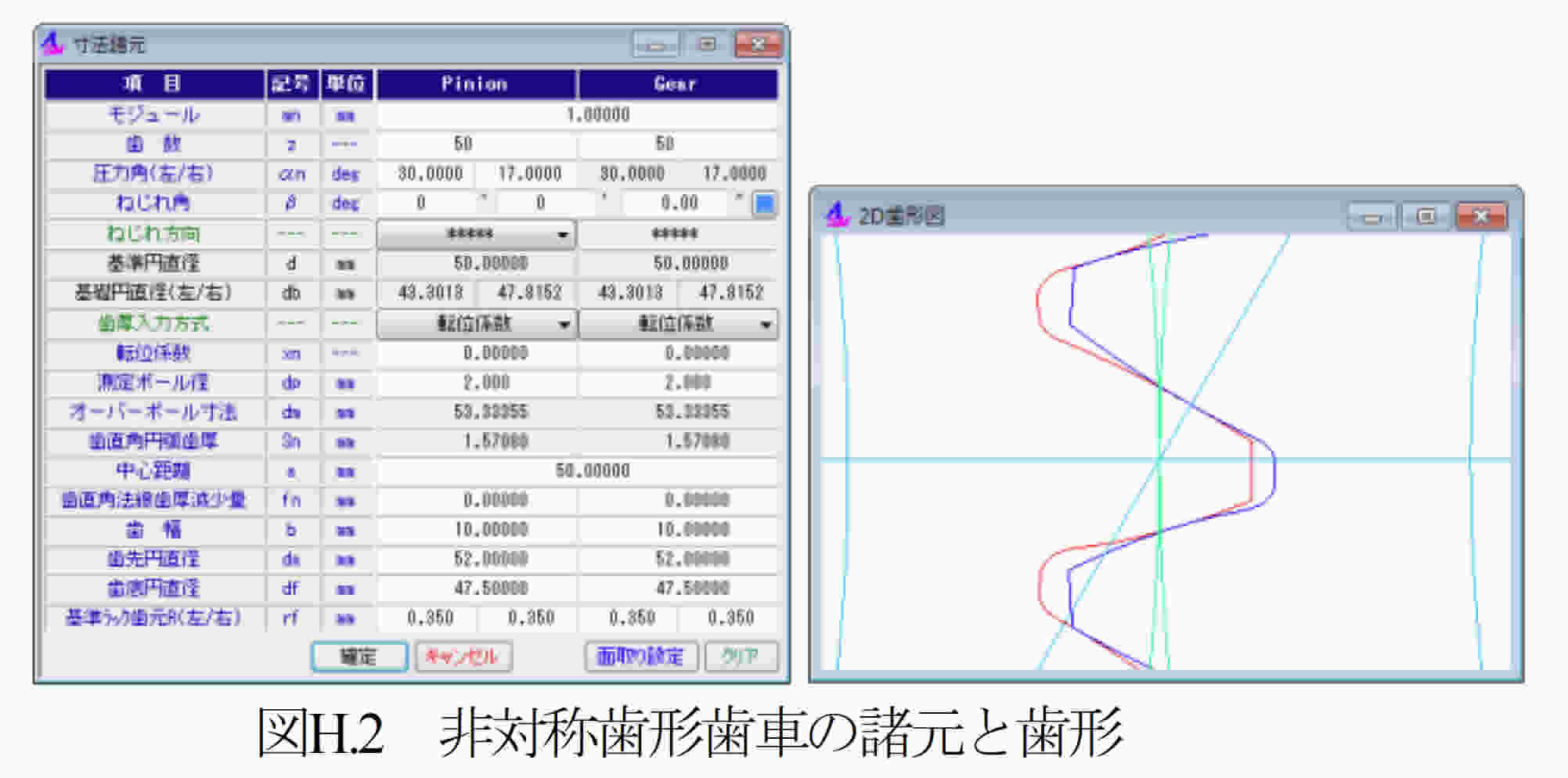
   圧力角が25°や27°の歯車は，製鉄所の圧延機のような高負荷歯車装置には曲げ強度の向上から採用されているが，非対称歯形歯車は作用歯面に高圧力角(30°以上)を有する歯形である．両歯面を高圧力角の対称歯形とすると歯先尖りとなるため歯形が成立しない．そのため歯たけを保つためには必然的に非対称歯形にする必要がある．その一例を図H2に示す．この例では，作用側圧力角αnR=30°, 反作用側圧力角αnL=17°,としている．高圧力角歯形は，標準圧力角(20°)に比べ，ヘルツ応力は大きく低下し，摩擦係数は小さく，すべり率は小さく，そしてフラッシュ温度を低く抑えることができる．しかし，この効果の代償として正面かみ合い率が低下したり軸受荷重が増加したりすることに留意する必要がある．これらの特性を持つ非対称歯形歯車のヘルツ応力，フラッシュ温度，曲げ応力などについて解析した結果について述べる．


H.2 高圧力角の効果
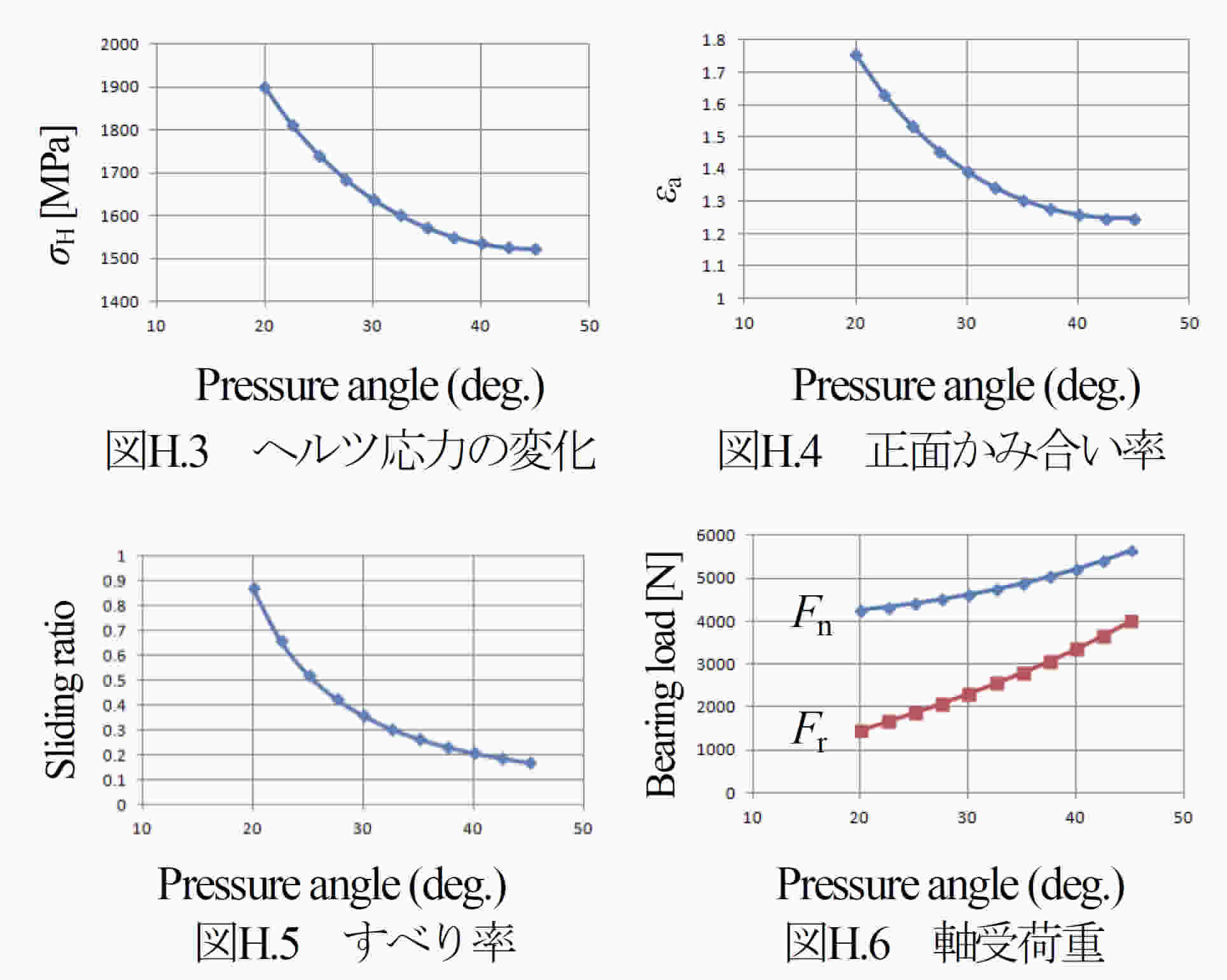
   かみ合い圧力角を大きくすることでヘルツ応力などが，どのように変化するかを検討する．検討する歯車諸元は，モジュールm=1, 歯数Z1=Z2=50, ねじれ角β=0° 転位係数Xn1=Xn2=0, 歯幅b=10mm, トルクT=100N･m, 回転速度n=1000min-1 とし，作用側圧力角αnRだけを20～45°の範囲で変化させて計算した．反作用側歯面の圧力角αnLは無視している．その結果，図H.3～H.6に示すように，かみ合い圧力角20°のときσH=1899MPaのヘルツ応力が圧力角35°では，σH=1573MPa（1/1.21倍）と低下し，すべり率も1/3.3倍小さくなっているが，正面かみ合い率は1/1.34低下するとともに軸受荷重Frは1.9 倍に増すことに注意しなければならない．


H.3 フラッシュ温度
   図H.2と同諸元で材料をSCM420（熱伝達率60.0[W/mK]），潤滑油をISO VG100, 油温70℃，歯面粗さRz2.5, Ra0.4, 回転速度1000～5000 min-1として図H.7のように設定し，摩擦係数(松本の式)2) およびフラッシュ温度3)を計算すると図H.8，H.9のようにいずれも圧力角 αn=20°よりαnR=30°のほうが有利であることが解る．また，回転速度5000min-1 においてフラッシュ温度は17.3℃低くなる．また，図H.10に圧力角の違いによるフラッシュ温度分布4)を示すが，αnR=30°のほうが9.7℃低いことが解る．


AMTEC  www.amtecinc.co.jp

195

H.4 高圧力角による負荷容量の向上
H.4.1 対称歯形歯車
   対称歯形歯車（α20°）の歯車諸元とかみ合い歯形を図H.11および図H.12に示す．歯形修整については図H.13のようにピニオンに歯先修整とクラウニングを与え，ギヤには歯先修整のみ与えている．以下に，歯面応力，フラッシュ温度そして歯元応力を計算をした結果を示す．

    解析条件は，図H.14のようにトルク300Nmとし，ピニオンに10μmのピッチ誤差を与え，図H.15のように食い違い誤差0.02°（平行度誤差0°）を与えている．歯面解析の結果を図H.16に，フラッシュ温度の設定と解析結果を図H.17およびH.18に示す．また，歯元曲げ応力（回転角θp=-23.52°）の解析結果を図H.19に，そして歯の変位（100倍）を図H.20に示す．


AMTEC  www.amtecinc.co.jp

196


H.4.2 非対称歯形歯車
   非対称歯形歯車の諸元を図H.21のように非対称圧力角（作用面αnL=30°，反作用面αnR=17°）として与えたときの歯のかみ合いを図H.22に示す．図H.23は，歯面応力が最も小さくなる歯面修整をソフトウェア機能の「歯面+修整量解析」から求めたものである．この歯形で歯面応力解析をした結果を図H.24に，フラッシュ温度を図H.25に示す．なお，歯面要素設定およびフラッシュ温度計算の設定は，図H.14，図H.17と同じである．また，歯元曲げ応力（ピニオン：回転角θp=-15.35°，ギヤ：θp=19.63°）の解析結果を図H.26に，そして歯の変位（100倍）を図H.27に示す．


H.4.3 対称歯形歯車と非対称歯形歯車の比較
   H4.1項およびH4.2項で計算した結果を図H.28に示す．これらを比較すると歯面応力，フラッシュ温度，そして歯元曲げ応力においても対称歯形より非対称歯形のほうが優位であることが解る．


AMTEC  www.amtecinc.co.jp

197

   図H.29に，かみ合い角度範囲内（図H.15）での歯元曲げ応力（最大主応力の最大値：σ1max）を示す．なお，回転角-10°～+20°付近で応力が小さくなっているのは，図H.14でピッチ誤差（10μm）を与えているためである．


   次に，寿命計算を図H.30に示すが，対称歯形（α20°）のピニオンの歯面寿命L(α20°)=1.36×106に対し非対称歯形（α30°）のピニオンの歯面寿命はL(α30°)=8.14×108と大きく寿命が延びていることが解る．


H.5 まとめ
  本例の非対称歯形（α30°）と，対称歯形（α20°）の歯面強さ，フラッシュ温度そして曲げ強さを比較すると
(1)歯面応力              ：σHmax=1897/2348=1/1.24
(2)フラッシュ温度       ：Tfmax=56.4-40.9=15.5℃低下
(3)ピニオン曲げ        ：σ1max=463/491=1/1.07
(4)ギヤ曲げ              ：σ1max=404/491=1/1.22
のように非対称歯形のほうが優位であることが解る．ただし，対称歯形（α20°）の歯面修整は，単純なクラウニングと歯先修整を与えただけであり非対称歯形歯車の歯面修整とは大きく異る．そのため，歯面応力やフラッシュ温度は歯面修整の効果も影響している．

H.6 補足1（無修整歯形）
  図H.11と図H.21の歯車で，歯面修整が無い歯車の歯面応力は，図H.31および図H.32のように対称歯形（α20°）のほうが1.2倍大きな応力が発生し，ピニオン歯元に大きな歯面応力が表れている．また，フラッシュ温度も図H.33のように対称歯形（α20°）のほうが18℃高い温度が発生し，その分布を見ると図H.33(a)ではピニオン歯先に大きな発熱部があり ，また歯元では歯すじに沿って発熱していることが解る．

これは，ピニオン歯元でトロコイド干渉が発生することを示唆している．


H.7 補足2（非対称歯形歯車の例）

  非対称歯形歯車の例を図H.34に示す．この歯車対は，ロシアのAsymmetrical gears - some of the TV7-117S turboprop engine gearbox components and assembliesであり実際に稼働している歯車である．

◆Webにも資料を掲載していますのでご覧ください.

参考資料
1) 久保愛三，日本歯車工業会説明会資料(2012)
2) 松本將，混合潤滑状態にある転がり-すべり接触面の摩擦係数推定式，トライ
   ボロジスト（日本トライボロジー学会誌），56巻，10号（2011-10）pp.632-638
3) AGMA2001-C95, Fundamental Rating Factors and Calculation Method for
   Involute Spur and Helical Gear Teeth, p.46
4) CT-FEM ASM, Gear design software, アムテック, (2014)
5) A.S. Novikov, V.V. Golovanov, D.V. Dorofeyev, "Desgn of Optimal
   Geometry, Stress, Stiffness, Vibaration and Terminology of Asymmetrical and
   HCR Gears for Aircraft", IFToMM), pp.139,(2014)

AMTEC  www.amtecinc.co.jp

198