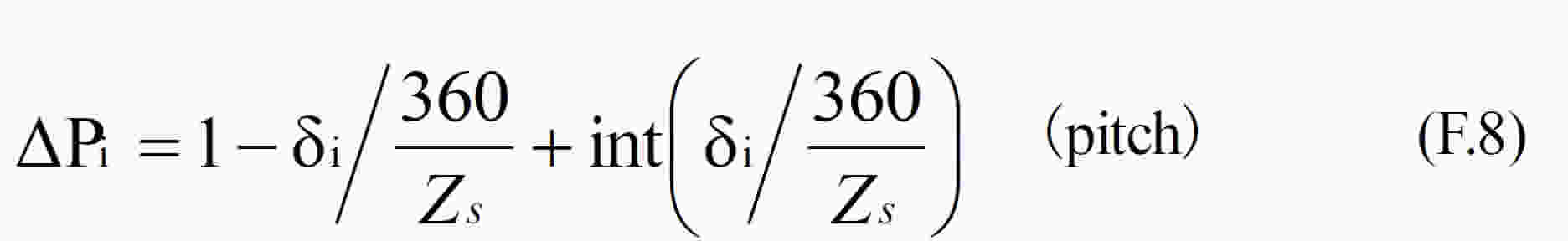遊星歯車設計のポイント

F1. はじめに
   遊星歯車は，サンギヤと複数個のピニオンおよびリングギヤから成る一種のギヤシステムであり，各ピニオン位置のかみ合いに位相を持たせることで，振動あるいはノイズ特性をコントロールすることができる．このかみ合い位相は，サンギヤ歯数，リングギヤ歯数とピニオン個数によって決まる．
   ここでは，かみ合い位相の種類とそれによる遊星歯車の振動騒音の特徴を整理して説明する．遊星歯車設計時の検討ポイントとして活用いただければ幸いである．

F2. 概要
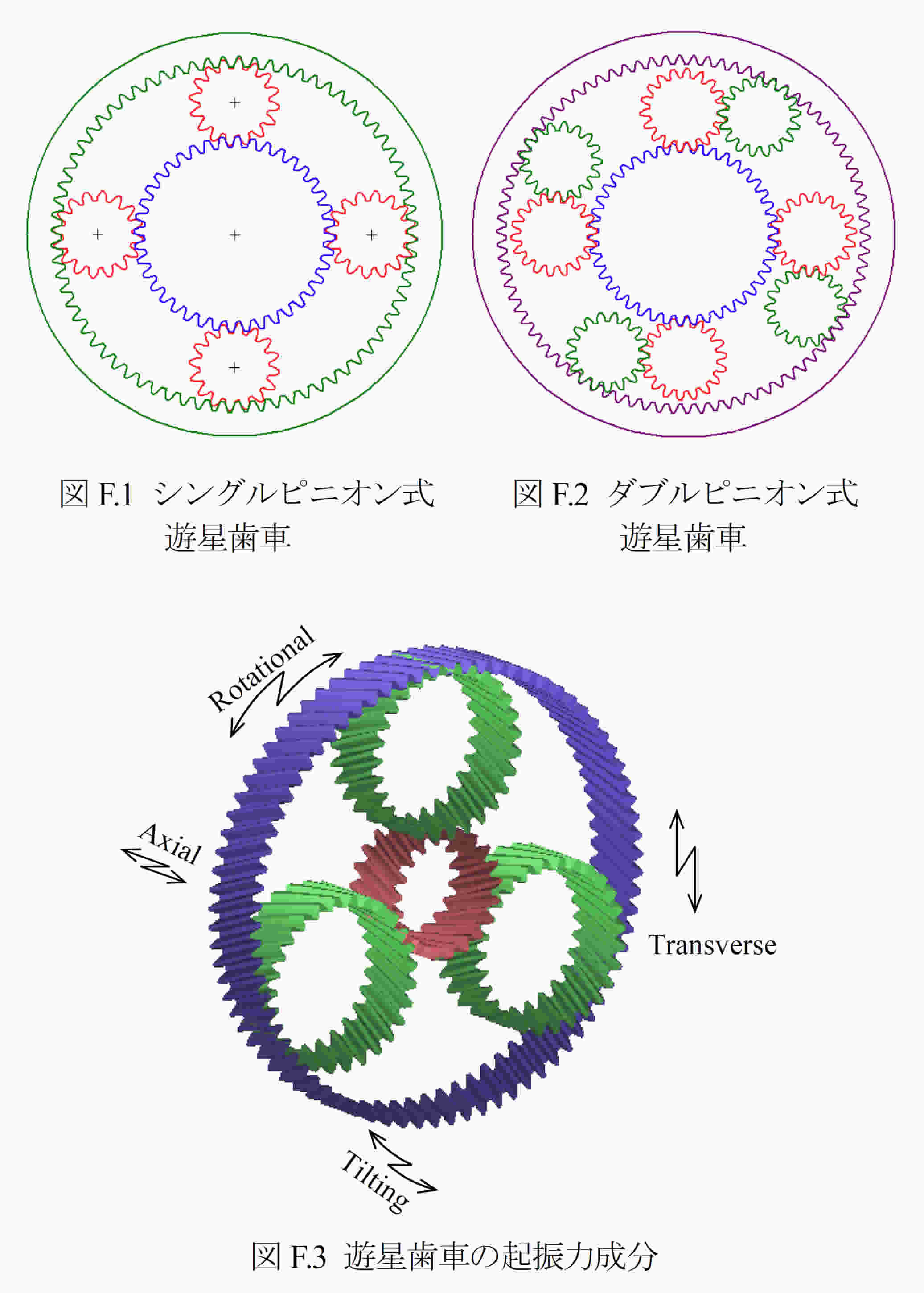
  遊星歯車機構は，シングルピニオン式遊星歯車(図F.1)とダブルピニオン式遊星歯車(図F.2)が基本となっている．自動車用自動変速機は，これらを組み合わせた複合遊星歯車として多段変速を実現している．この基本となるシングルピニオン式遊星歯車とダブルピニオン式遊星歯車について，サンギヤ歯数，リングギヤ歯数とピニオン個数とかみ合い位相の関係およびかみ合い位相と遊星歯車の起振力の関係を以下に整理する．なお，遊星歯車の起振力 は，図F.3に示すように回転方向(Rotational)，半径方向(transverse)，軸方向(Axial)と倒れ方向(Tilting)の4 つの方向の成分を持つ．かみ合い位相によりこれら4つの方向の成分がそれぞれ影響を受けることになる．

          (1+λ)N_c=N_r+λN_s                                      (F.1)

②ダブルピニオン式遊星歯車

          (1-λ)N_c=N_r-λN_s                                      (F.2)

ここに， λはサンギヤ歯数Z_sとリングギヤ歯数Z_r の比で

           λ=Z_s /Z_r＜1である．

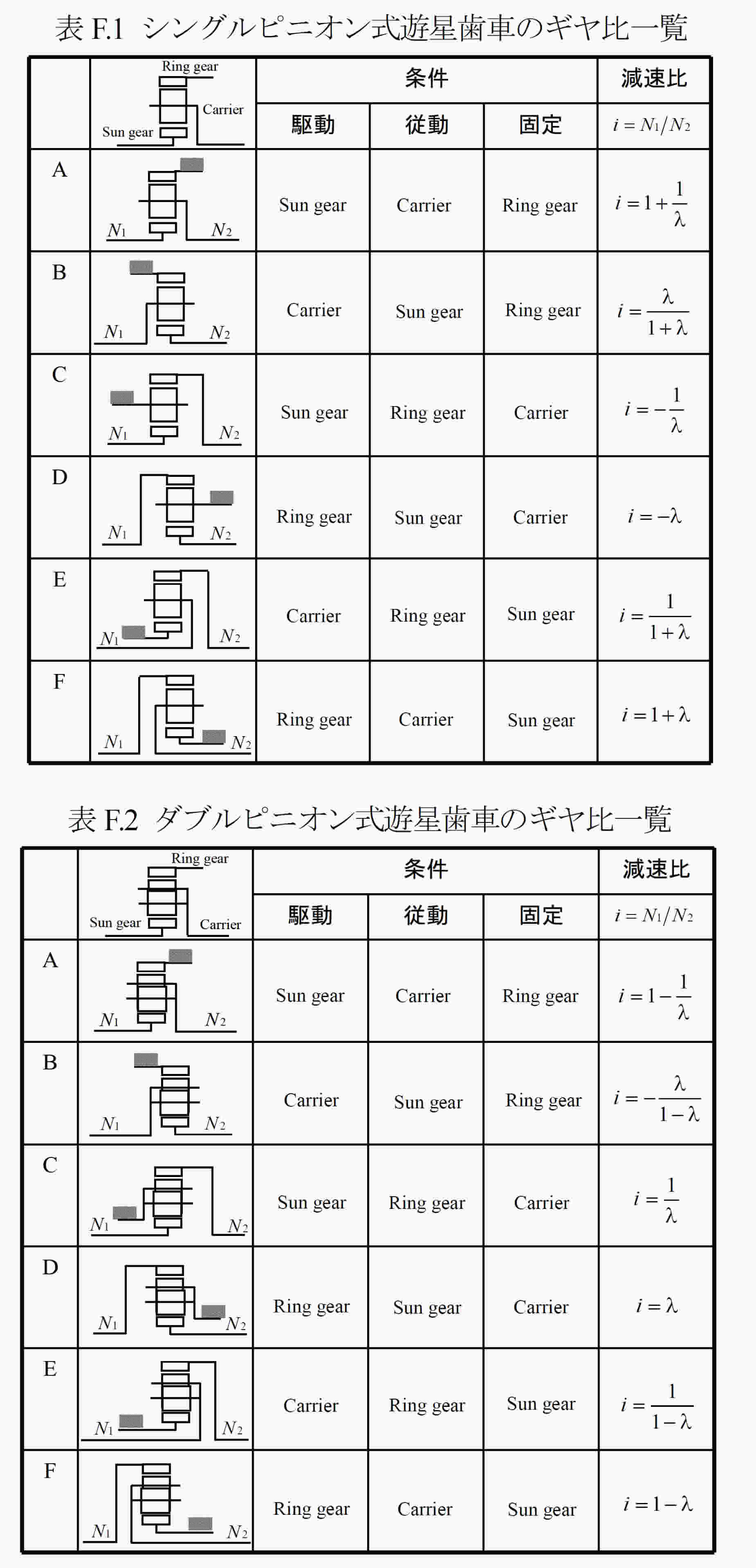
  式(F.1)，（F.2)から3 つの回転要素のいずれかを固定，いずれかを入力，残りを出力とすることであるギヤ比が求まる．表F.1および表F.2は，シングルピニオン式遊星歯車とダブルピニオン式遊星歯車のギヤ比を運転条件に合わせて整理したものである．
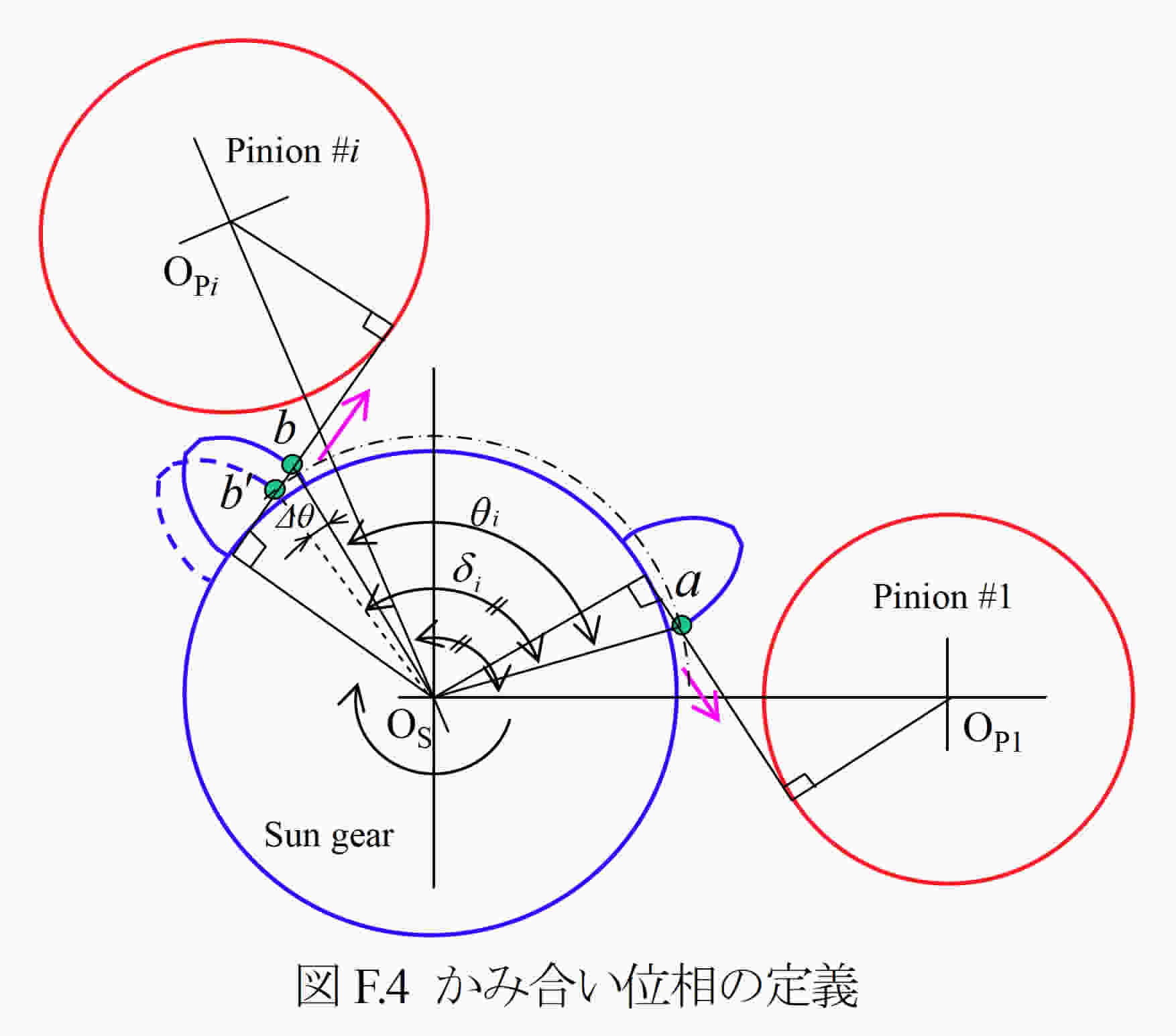
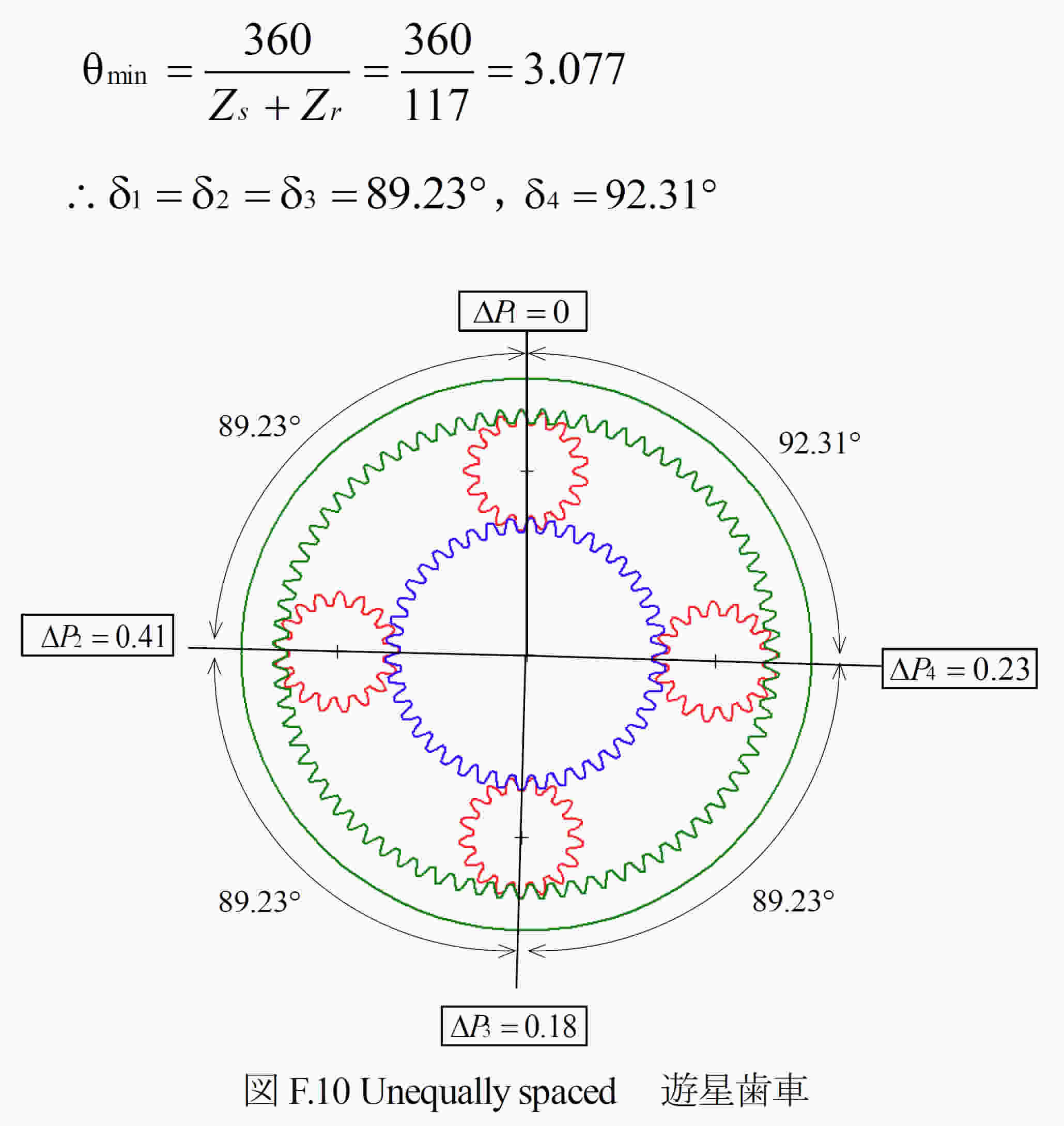
F4. 遊星歯車の配置角
   ピニオンの配置角δは，サンギヤ歯数Z_s，リングギヤ歯数Z_rとピニオン個数k_p

AMTEC  www.amtecinc.co.jp

F5. かみ合い位相の定義
   かみ合い位相とは，各ピニオン位置でのかみ合いのタイミングのずれのことである．たとえば，図F.4において，サンギヤの歯元とピニオン# 1 の歯先がかみ合っているとき(点a )，i 番目のピニオン#i もサンギヤの歯元とピニオンの歯先がかみ合っていれば(点b' )，かみ合いのタイミングのずれ，すなわち，かみ合い位相はないということになる．しかし，実際にはサンギヤの歯は等間隔に配置されているのでピニオン#i はサンギヤと点b でかみ合うことになる．ピニオン#i の点b でのかみ合いは，ピニオン#1 の点aのかみ合いに対してΔθ進んでいることになる．

F6. かみ合い位相と起振力特性
  各ピニオン位置でのかみ合いの位相は，サンギヤ歯数Z_s，リングギヤ歯数Z_rとピニオン個数k_pの設定で決まり，以下の5 つのパターンに分類される．位相のパターンにより，回転方向(Rotational)，半径方向(Transverse)，軸方向(Axial)および倒れ方向(Tilting)それぞれの起振力特性が影響を受ける．
① ピニオン位置のかみ合いに位相差がない場合 (In phase)；位相差がなく各ピ
    ニオン位置でのかみ合いは同一のタイミングとなるので，回転方向および軸方
    向の起振力はピニオン個数倍となり，その変動成分は大きくなる．一方，半径
    方向および倒れ方向の起振力は釣り合うので，変動成分は小さくなる．
  この状態は以下のギヤ構成条件で作り出される．

        (Z_s+ Z_r)/k_p= integer (整数)― ピニオン等配置

        Z_s/K_p=integer (整数)

        例：Z_s=33，Z_r=75，K_p=4の遊星歯車(図F.5)

②各ピニオン位置でのかみ合いの位相が1/ k_pピッチずつ順番にずれる場合

AMTEC  www.amtecinc.co.jp

        Z_s/K_p≠integer (整数)で，小数点以下が1/ _{k p} or 1-1/ _{k p}

        例：Z_s=33，Z_r=75，K_p=4の遊星歯車(図F.6)

        (Z_s+ Z_r)/k_p= integer (整数)― ピニオン等配置

        Z_s/K_p≠integerで，小数点以下が0.5

        例：Z_s=30，Z_r=74，K_p=4の遊星歯車(図F.7)

④各ピニオン位置でのかみ合いの位相が2/k_p or1-2/k_pピッチずつ順番にずれる場合(Optimum phase)；ピニオン個数が5or 6の場合この条件も存在する．
k_p = 5の場合，回転方向，軸方向，半径方向および倒れ方向すべての起振力が，5 つのピニオン位置すべてのかみ合いで相殺されるので，その変動成分を小さくすることができる．また，歯面誤差や組付け誤差による起振力の相殺度合いは影響されにくくなる．k_p=6の場合，対向するピニオン位置のかみ合いは同位相となる ので，3 つのピニオンのかみ合いで回転方向，軸方向，半径方向

        (Z_s+ Z_r)/k_p= integer (整数)― ピニオン等配置

        Z_s/K_p≠integerで，小数点以下が2/K_p or 1-2/K_p

        例：Z_s=37，Z_r=78，K_p=5の遊星歯車(図F.8)

        例：Z_s=38，Z_r=82，K_p=6の遊星歯車(図F.9)

AMTEC  www.amtecinc.co.jp

        例：Z_s=42，Z_r=75，K_p=4の遊星歯車(図F.10)

     最小かみ合い角θ_minは，

(寄稿 森川 邦彦)

AMTEC  www.amtecinc.co.jp