[付録：E] 正弦歯形歯車の動力損失低減の可能性

[付録：E]
正弦歯形歯車の動力損失低減の可能性
E.1 緒言
1980年代初め頃よりAV機器などに盛んに使われ始めたプラスチック歯車は，鋼歯車の設計基準に倣ってインボリュート歯形が採用されている．プラスチック歯車を低トルク領域での動力伝達や回転伝達のみを目的とする場合はインボリュート歯形を採用することに全く異論は無い．しかしながら，ある程度大きなトルク領域での動力伝達に用いられた場合は，プラスチック材料の弾性率が鋼材料の1/70 ～ 1/100 と小さいことに起因するかみ合い時の歯の大きな変形のため，幾何学的なインボリュート歯車のかみ合いから，鋼歯車に比べて大きく外れているものと思われる．したがって，インボリュート歯車の最大の長所の一つ，中心距離鈍感性の優位性はそれほど期待できず，インボリュート歯形に固執する必要はないのではないだろうか．一方，地球環境問題は言うに及ばず，機器の小型化や軽量化，多機能化に伴い，駆動系の電力配分が制限されている現状を考慮すると，たとえ僅かであってもエネルギ損失の低減が期待できるならば，インボリュート以外の歯形の採用も十分検討に値するものと思われる⁽¹⁾．
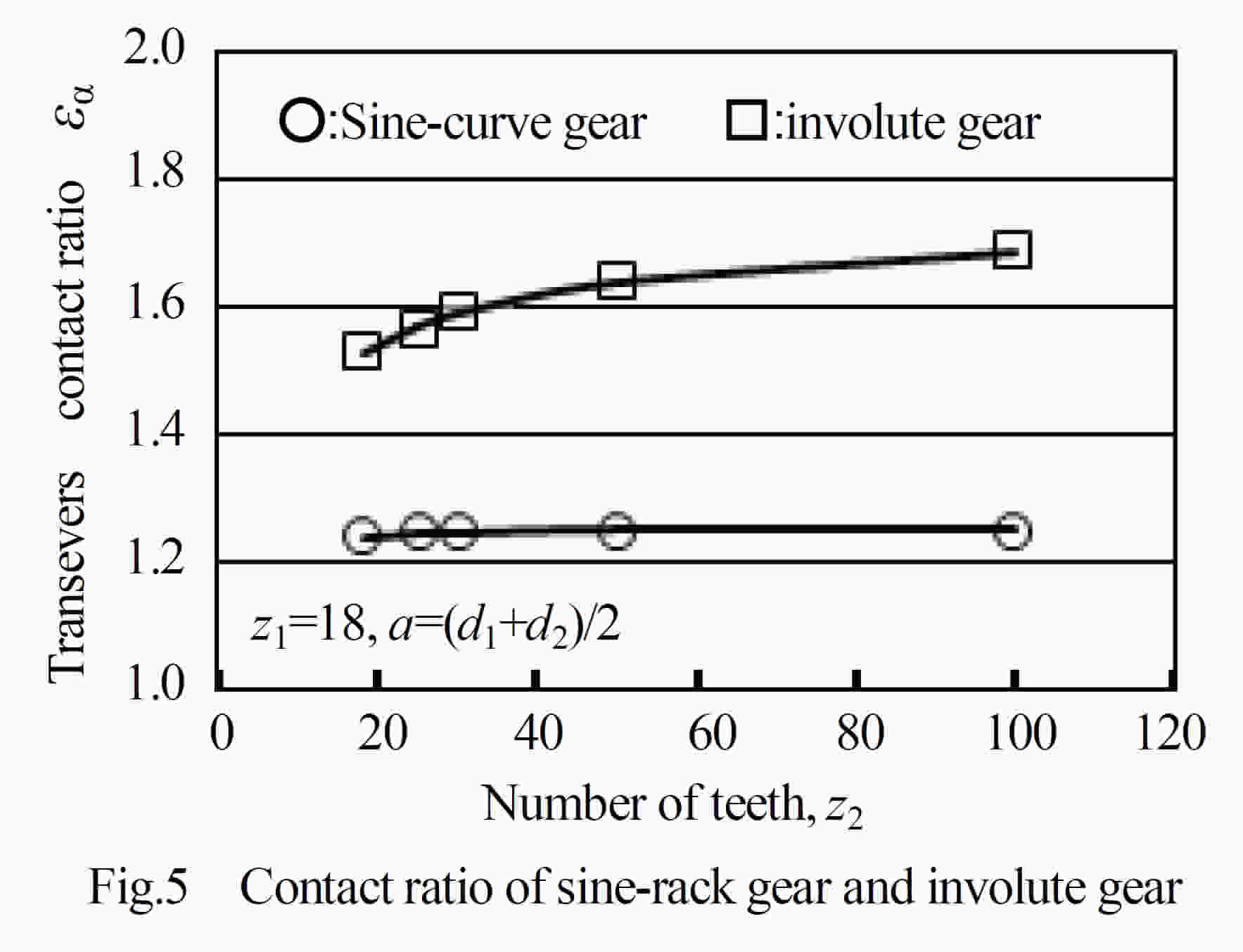
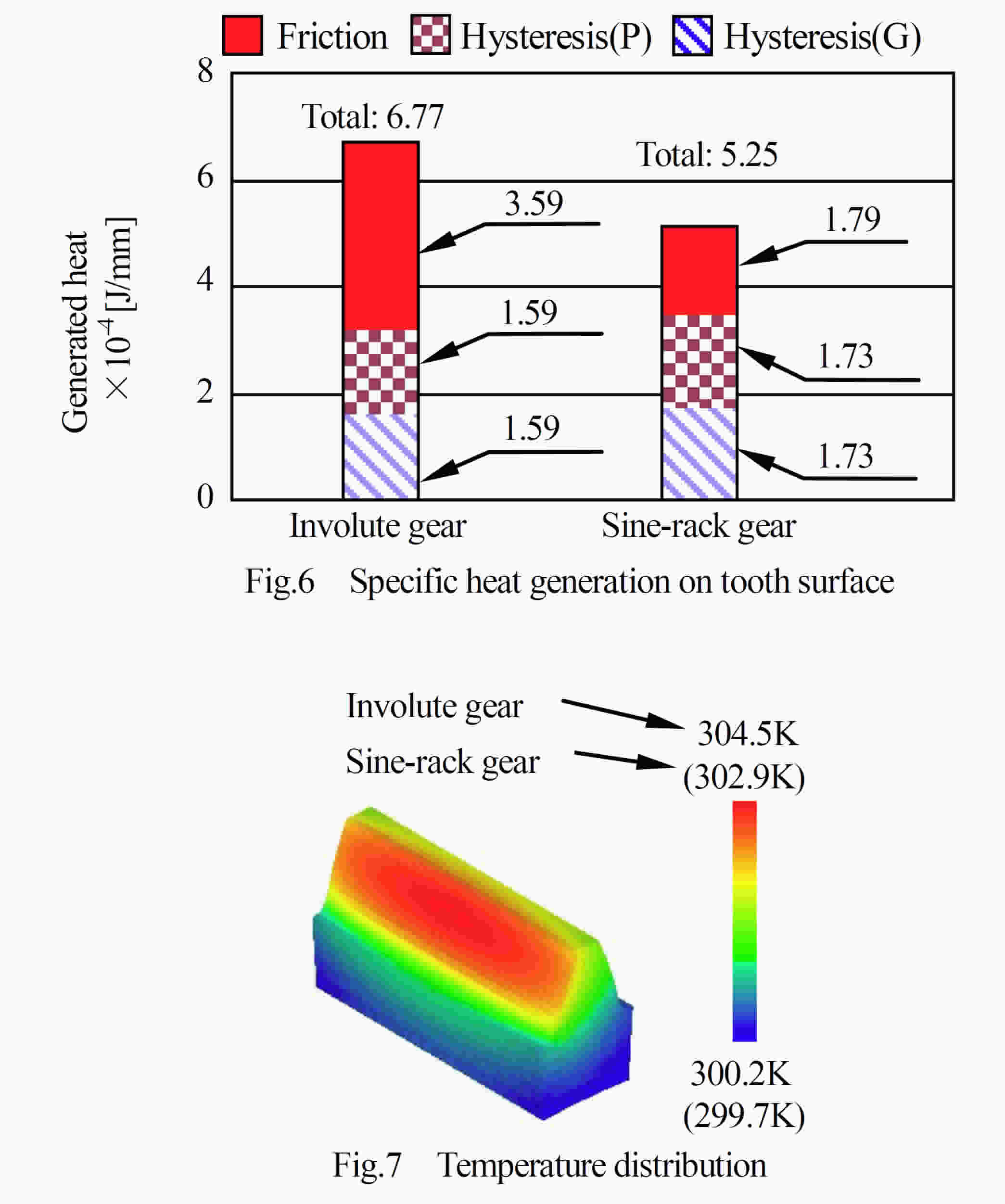
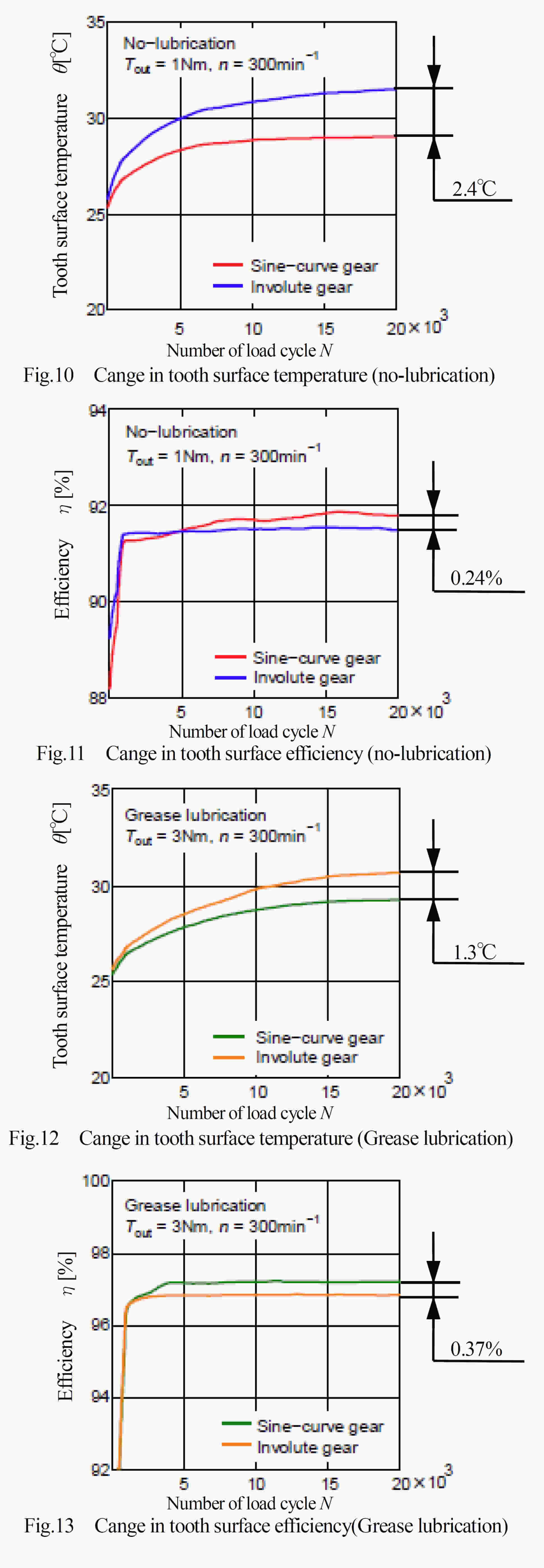
そこで，正弦曲線で構成される歯形を基準ラックとする歯車（以下，正弦歯形歯車[sine-rack gear]と呼ぶ）が，インボリュート歯車（直線ラック歯車）に比べ，すべり率が小さくなることに着目し，正弦プラスチック歯車による動力損失低減の可能性について検討する．さらに，動力損失が小さくなるとかみ合い時の発熱量が減少し，歯の温度上昇も押さえられる．したがって，温度上昇に伴うプラスチック材料の許容曲げ応力の低下も小さくなり，結果として，プラスチック歯車の負荷容量の増加も期待できる．また，同時に，正弦ラック歯車のかみ合いは，インボリュート歯車に比べ，かみ合い点における相対曲率が小さく，また，歯の幾何形状についても歯元のすみ肉部の歯厚が大きいことなどが歯面接触応力，歯元曲げ応力の低下をもたらし，負荷容量増加に有利に働くことも期待できる．本稿では，正弦歯形歯車の発熱や効率について検討し，運転試験を行い検証した結果について述べる．

E.2 正弦曲線で構成される基準ラック
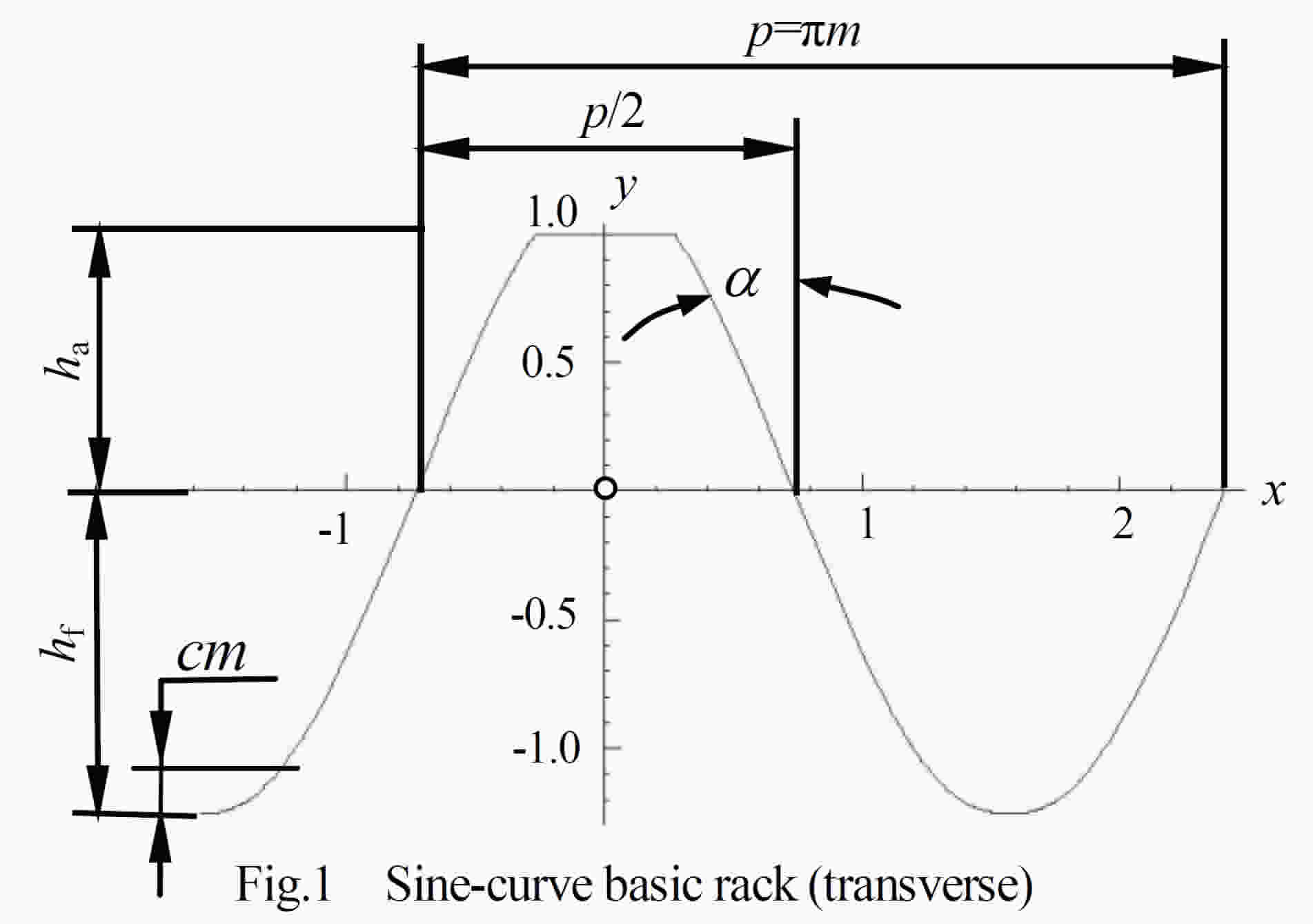
本件では，正弦曲線で構成される基準ラック（正弦[曲線基準]ラックと呼ぶ）を図 1のように定義する．データムは，歯形および歯底を構成する正弦曲線の対称軸に一致させ，ピッチをπm（m:正面モジュール）とする．歯末のたけh_aをm，頂げきを cm( c :頂げき係数0.25)として歯元のたけ h_f を (1 + c)m とする．また，正弦歯形歯車は，インボリュート歯車と異なり，幾何学的には中心距離を調整することによりバックラッシを与えることができない．したがって，基準ラックの左右両歯面をそれぞれデータム線に沿って逆方向にシフトさせる（以後，横転位という）ことによって与える必要がある．そこで，歯厚減少量（これが基準円上のバックラッシとなる）をc_jm（c_j : 歯厚減少係数と呼び 0.1を標準とする）とする．このように定義し，図 1 のように座標系をとると，歯先面および歯底面部分を除いて，θ（左歯面は -1.5πm≦θ≦0，右歯面は，0< θ≦1.5πm ）をパラメータ（-π/2≦θ≦2π）とすると基準ラック歯面の座標は，式(1)および式(2)で，また，デ

ータム線上の正面圧力角は，式(3)で表すことができる．
X=m(θ/2±C_j/2)[mm] (1)

y=m(1+C)・sin(θ+π/2)[mm] (2)

α=π/2-tan^-1(2h_f/m)[rad] (3)

ただし，式(1)の復号の上は左歯面，下が右歯面を表す．このように，歯元フィレット部を含めてそれぞれ一つの正則関数で表すことができることも一つの特徴であり，かみ合い機構解析が容易に行えることを示唆している．一方，歯数zの基準円d，すなわち歯切りピッチ円直径を，これもインボリュート歯車に倣い正弦基準ラックのピッチをπm としているので，

d=zm (4)

と定まる．正弦ラックでも，当然，転位は可能である．しかしながら，転位（rack shift）すると歯切りピッチ線がラックのデータムに一致しなくなる．従って，正弦曲線基準ラックはインボリュート歯車の基準ラックである直線歯形とは異なるため任意の歯切りピッチ線に対して対称となる歯形とはならない．そのため，対となる歯車の歯切りピッチ線の位置を一致させるためには対となる歯車の転位係数の和は常に0でなければならない．

E.3 正弦歯形歯車とインボリュート歯車の歯形比較
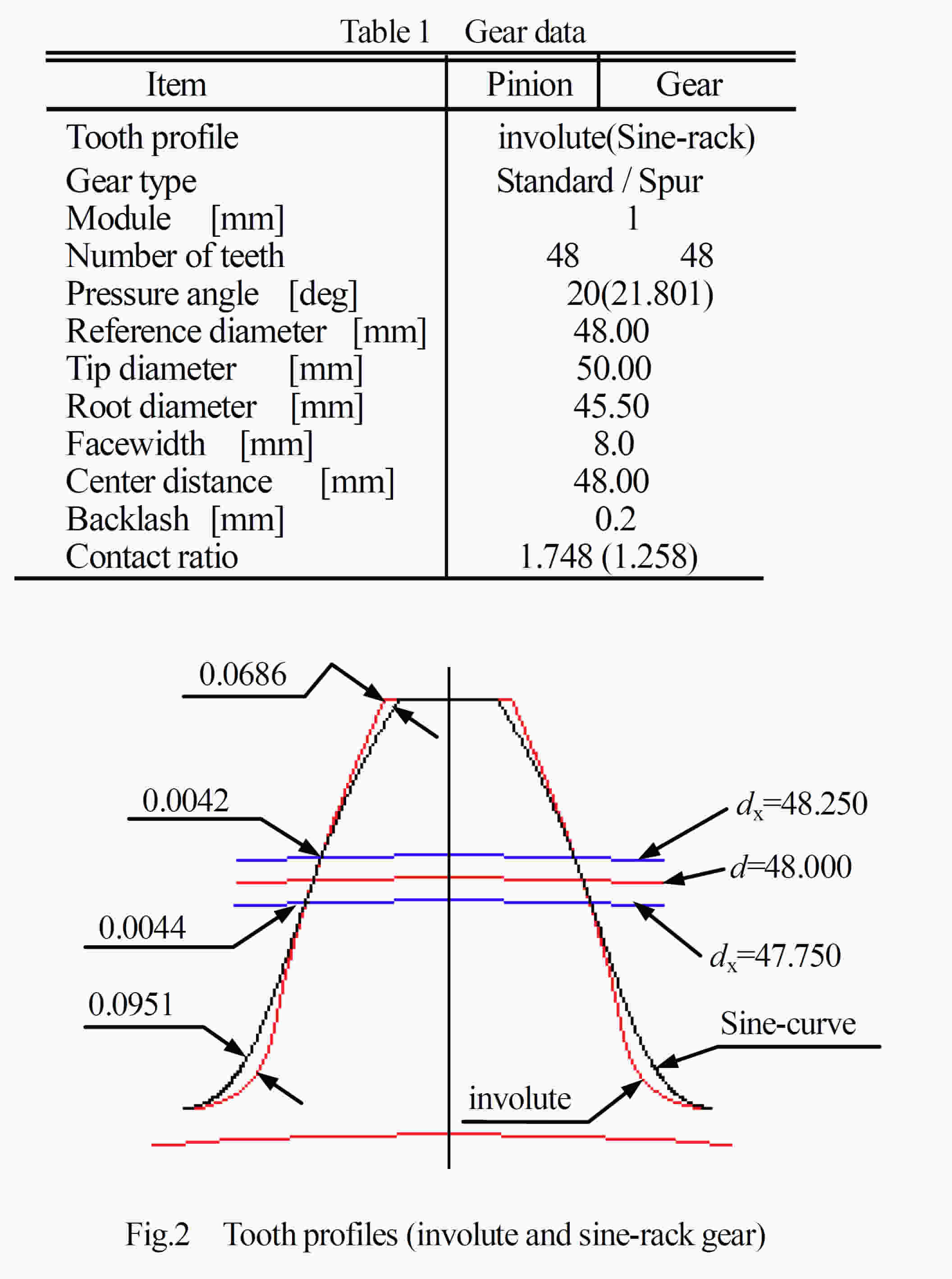
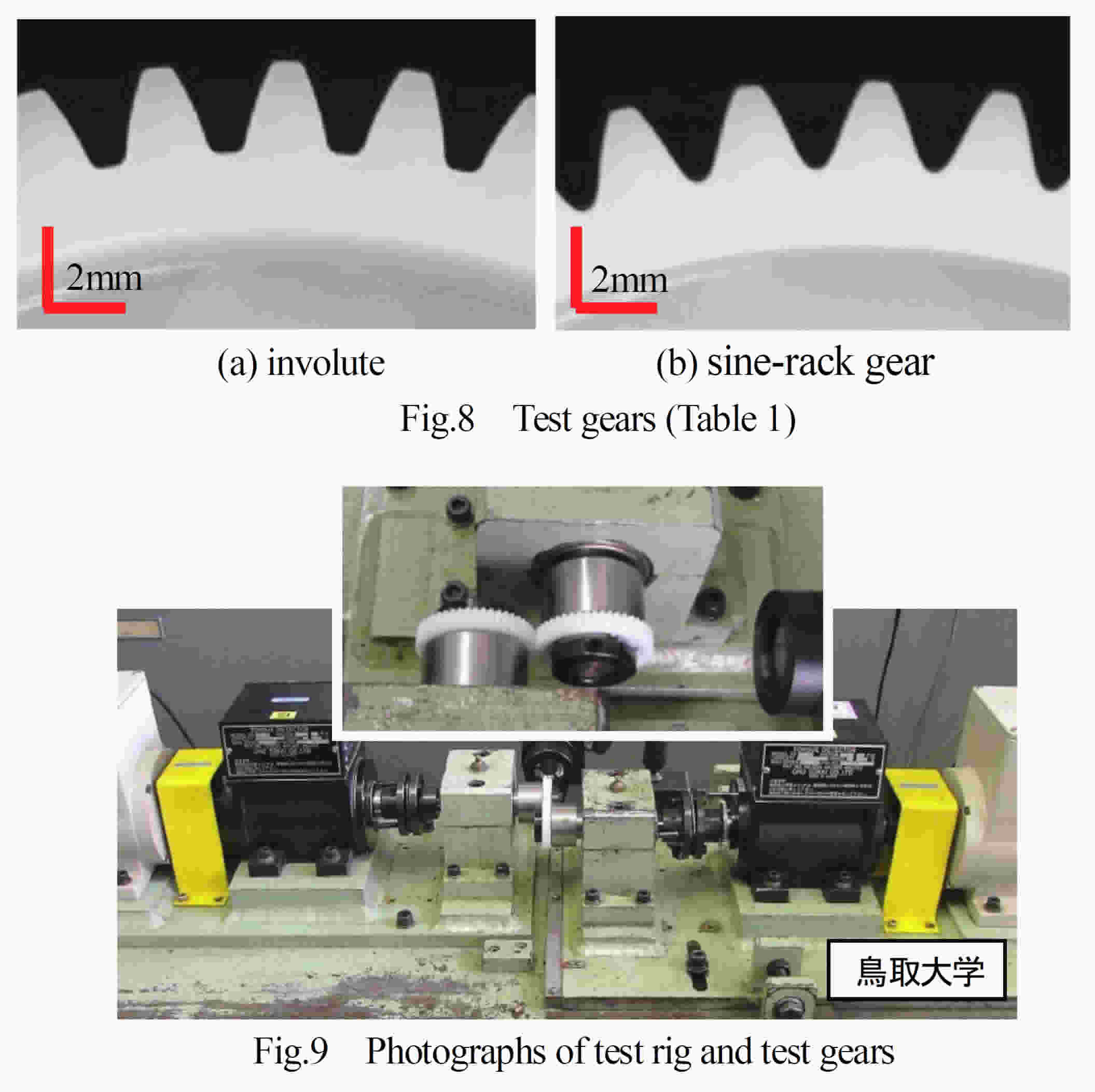
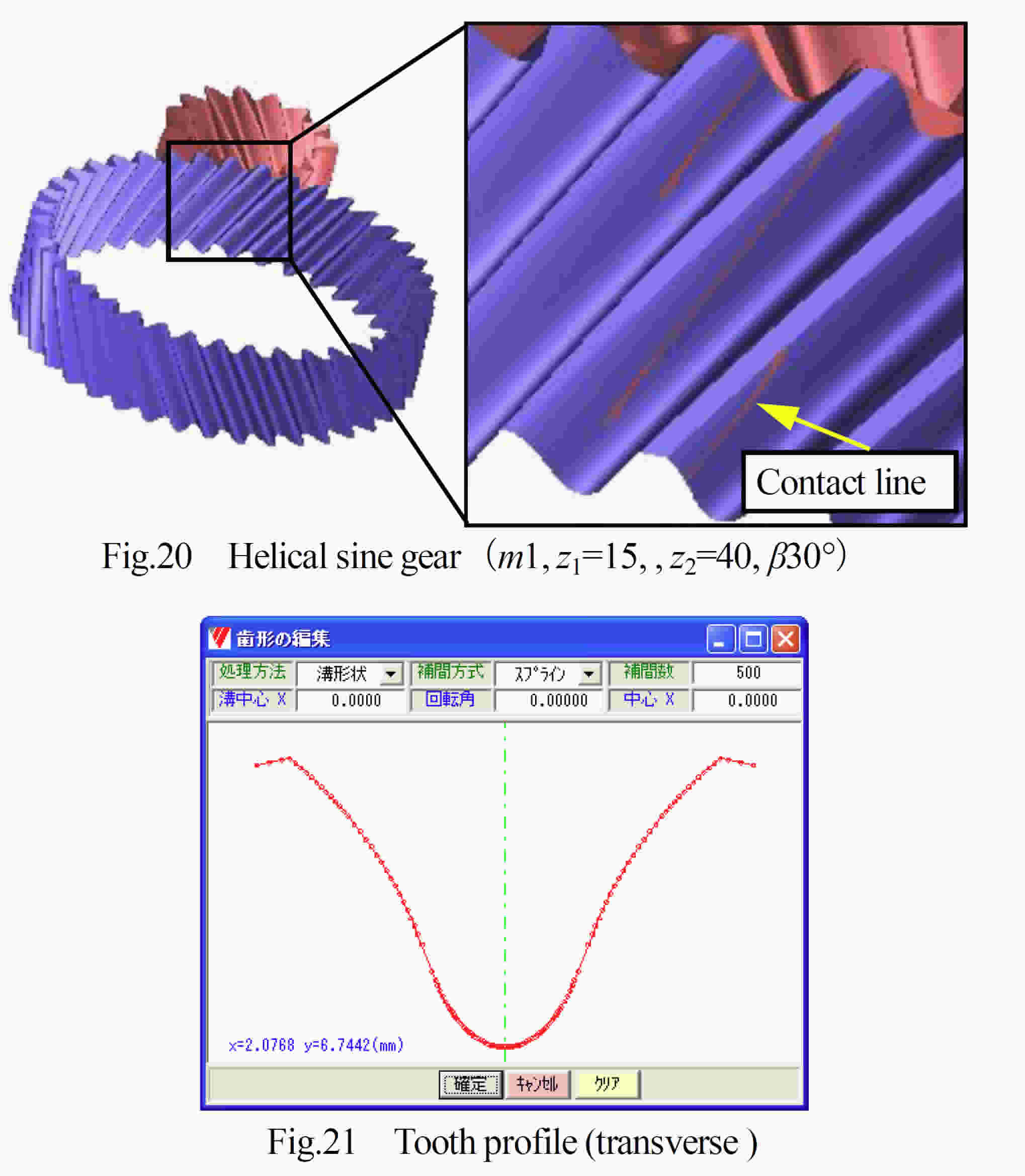
表1に示すインボリュート歯車と正弦歯形歯車について歯形⁽²⁾の比較を行う．両歯車の諸元（m, z, d_a, d_f ）を一致させるため正弦歯形歯車の歯元のたけ係数をh_f=1.250とした．そのため正弦歯形歯車の圧力角は21.801°である．なお，正弦歯形はインボリュート歯形と同様，正面を基準とする．インボリュート歯車と正弦歯形歯車は図2に示すように正弦歯形歯車のほうが歯元で0.0951mm大きく，歯先では0.0686mm小さい．また，基準円直径付近の歯厚は，直径d_x=48.250mmでは正弦歯形歯車のほうが0.0042mm小さくd_x =47.750mmでは0.0044mm大きい．しかし，正弦歯形歯車の歯元のたけ係数をh_f=1.3737として正弦歯形歯車の圧力角を20°とした場合はd_x=48.250mmでその差は0.0002mmと微小である．

AMTEC www.amtecinc.co.jp

184

E.4 すべり率
かみ合う二つの歯車の歯面間に生じるすべり速度v_sは，接触点の軌跡上の任意の点におけるそれら二つの仮想ラック（基準ラック）に対する相対速度v_p及びv_gの和で与えられる．したがって，すべり率ξ_p及びξ_gは，それぞれ，

で与えられる．
表1の正弦歯形歯車とインボリュート歯車のすべり率を図3に示すが，インボリュート歯車の最大すべり率は，グラフの両端，すなわち，かみ合い始めと，かみ合い終り（ピニオン回転角φ=±6.22°）で最大値となるが，正弦歯形歯車は，かみ合い始めと，かみ合い終り（ピニオン回転角φ=±4.72°）ではなく，それより小さいφ= ±4.38°で最大値を示す．また，インボリュート歯車と正弦歯形歯車のすべり率を比較すると，インボリュート歯車の最大すべり率は0.745であり，正弦歯形歯車の最大すべり率は0.371であるであるため正弦ラック歯車の最大すべり率はインボリュート歯車の50%である．

E.5 かみ合い率
正弦ラック歯車のかみ合い率ε_αは，図4に示すように

であり，B_p,B_g は，それぞれピニオンおよびギヤの歯先と接触点軌跡の交点である．また Oi は，ピニオンおよびギヤの回転中心である．

図5は，ピニオンの歯数を18と固定してギヤ歯数を変化させたときのかみ合い率の変化の様子をインボリュート歯車のそれと比較して示したものである．値を見ると正弦ラック歯車のかみ合い率は，歯数にかかわらず大きく変化せず，インボリュート歯車のかみ合い率よりも小さくなることが分かる．試みに，z₁ = z₂ = 999として計算したところ，その正面かみ合い率は ε=1.258 とほとんど変化しない．なお，かみ合い率の計算に用いる中心距離は，a=(d₁+d₂)/2 としている．

AMTEC www.amtecinc.co.jp

185

E.6 発熱量
プラスチック歯車の発熱⁽³⁾は，負荷かみ合い時において歯面間の摩擦による発熱と材料が粘弾性体故のヒステリシス発熱を熱源とし，歯の温度は，負荷の大きさ，回転速度そして歯面間のすべり速度の影響を受け，運転時の平衡温度は，モジュール，歯幅そして回転速度による熱伝達係数により決まることになる．このことより，表1 のインボリュート歯車および正弦歯形歯車の発熱量について検討すると，インボリュート歯車の発熱量は表2の計算条件下では図6に示すように摩擦発熱量は3.59×10^-4 J/mmであり，ヒステリシス発熱はピニオン，ギヤそれぞれ1.59×10^-4 J/mmであることから総発熱量は6.77×10^-4J/mm となる．また，正弦歯形歯車の摩擦発熱は 1.79×10^-4 J/mm であり，ヒステリシス発熱量は，かみ合い率が小さいためインボリュート歯車より多くなり1.73×10^-4 J/mm となる．このことより正弦歯形歯車の発熱量は5.25×10^-4 J/mm と見積ることができるため，正弦歯形歯車はインボリュート歯車の77.5%の発熱量であると推定することができる．そして，図6に示す発熱量と表2 の計算条件から負荷運転時の歯の平衡温度を3 次元発熱・熱伝導解析ソフトウェア⁽⁴⁾で計算すると，図7に示すようにインボリュート歯車の歯面最大温度304.5Kに対し，正弦歯形歯車の歯面最大温度は302.9K となり1.6K低下することが分かる．

E.7 実験による検証
E.7.1 試験歯車および実験装置
表1 および図8のインボリュート歯車および正弦歯形歯車（共に射出成形品，材料はポリアセタールコポリマ）を図9に示す動力吸収式歯車試験機と試験歯車を用いて運転試験を行った．

実験は，いずれの歯車に対しても負荷トルク1Nm，回転速度300min^-1，バックラッシ0.2mm，無潤滑およびグリス潤滑の条件下で行った．運転中の歯の表面温度は赤外線放射温度計（キーエンス社製：IT2-02 型）を用いて，上方と水平方向からの2ヶ所で測定した．また，効率計測のための駆動および被動軸のトルクはトルクメータ（小野測器社製：SS-200型）で測定した．

E.7.2 実験結果
無潤滑での歯面温度を図10に効率の測定結果を図11に示す．図7の温度上昇の計算では1.6K低下すると見積もったが，図10の実験結果では正弦ラック歯車の温度上昇は，インボリュート歯車より2.4K低下し，効率は図11のように0.4% 良くなっている．

AMTEC www.amtecinc.co.jp

186

また，グリス潤滑の測定結果を図12および図13に示す．

E.8 片歯面かみ合い試験
表1の正弦歯形歯車を鋼製歯車で製作（成形研削）し，中心距離を理論よりも+0.1mm離した48.100mm とし，図14の伝達誤差試験機（小笠原プレシジョン，MEATA-3 型）で回転伝達誤差を評価した．その結果は図15に示すように，精度等級は，JIS N1 級（JIS B 1702-1:1998）であり非常に高精度であることが解る．

この歯車を正弦歯形歯車ソフトウェア（カタログ[32]）で回転伝達誤差を解析（a=48.100mm）すると図16および図17のように評価することができる．

E.9 歯車検査
インボリュート歯形（m_n1, z=48, α_n= 21.801°）として計測した結果を図18に示す．この歯形誤差グラフは，インボリュート歯形を基準としているためS 字のように表されるが，正弦歯形の座標値が既知であるため，インボリュート歯形との差異からJIS B1757-2（球基準器又は円筒基準器を用いた歯形測定）のように考えることにより評価が可能である（図19参照）．

AMTEC www.amtecinc.co.jp

187

E.10 正弦歯形はすば歯車の研削
正弦歯形はすば歯車（図20参照）の研削は，図21のように正面歯形が既知であれば，成形研削盤（カタログ[44.1]）により研削が可能である．図22に3次元干渉を考慮した成形研削用砥石形状を，図23に砥石と歯形の重ね合わせ図を示す．

E.11 結言
(1) 実験結果より潤滑の有無に関わらず正弦歯形歯車はインボリュート歯車より
    発熱量が小さいため動力損失を低減できる可能性を持つことが解った．
(2) 本稿で示した実験結果は，初期実験のみであるため，今後は多くの実験数
    で検証する必要がある．また，中心距離変動に対する回転伝達誤差や，負荷
    容量の実験検証を計画している．

E.12 参考文献など
(1) 上田昭夫，吉原正義，中村守弘，森脇一郎，正弦曲線で構成される歯形を
    基準ラックとするプラスチック歯車，日本機械学会，第10回機素潤滑設計部
    門講演会講演論文集，pp.123-126
(2) Gear Design Software Manual, Sine-Gear Design Software, (2009),アムテック
(3) 上田昭夫，吉原正義，高橋秀雄，森脇一郎，“プラスチック歯車のかみ合い
    発熱コンピュータシミュレーション” 日本機械学会論文集C 編，，Vol. 73, No.
    732(2007), p. 2361
(4) 上田昭夫，高橋秀雄，中村守弘，森脇一郎，“プラスチック歯車のかみ合い
    発熱コンピュータシミュレーション”，（歯の温度上昇に及ぼすモジュールと回
    転速度の影響），日本機械学会論文集C編，Vol. 75, No. 752(2009),
    p. 1074

AMTEC www.amtecinc.co.jp

188