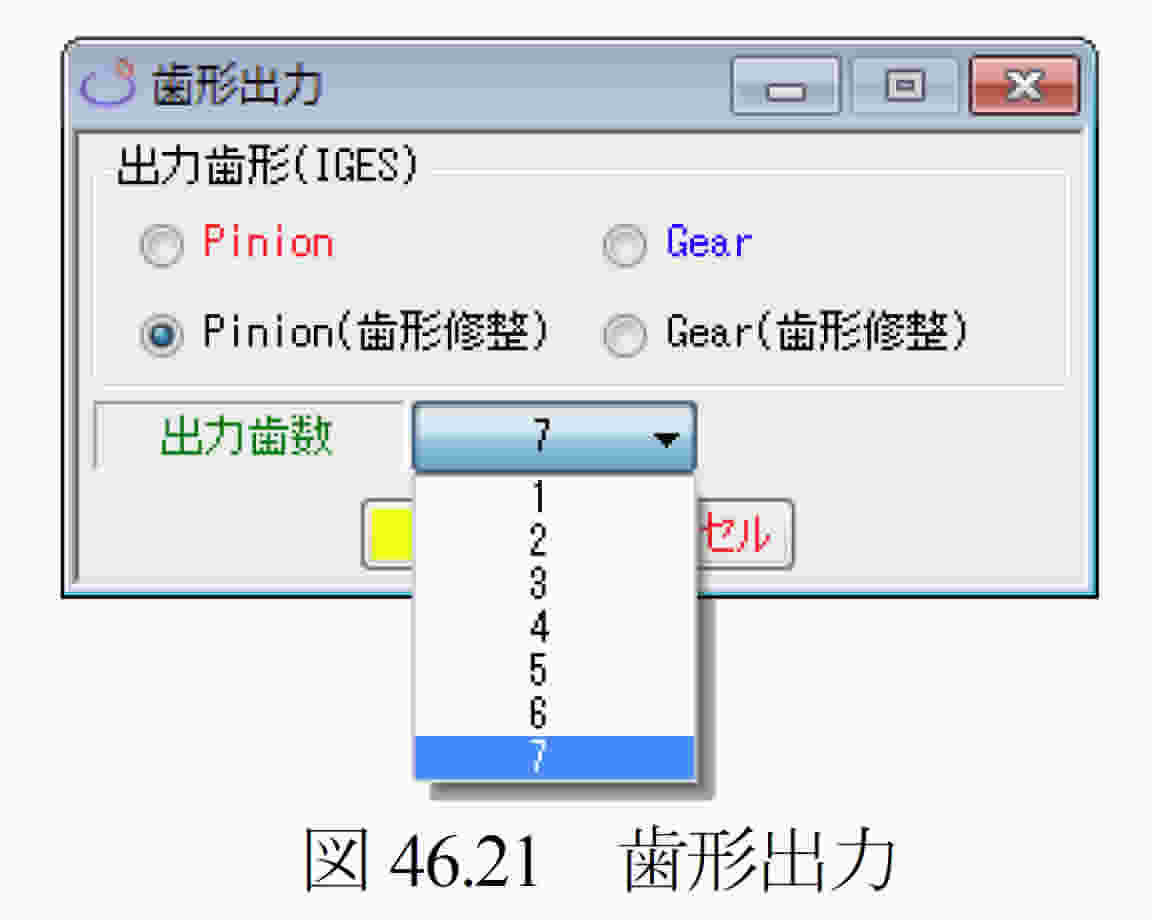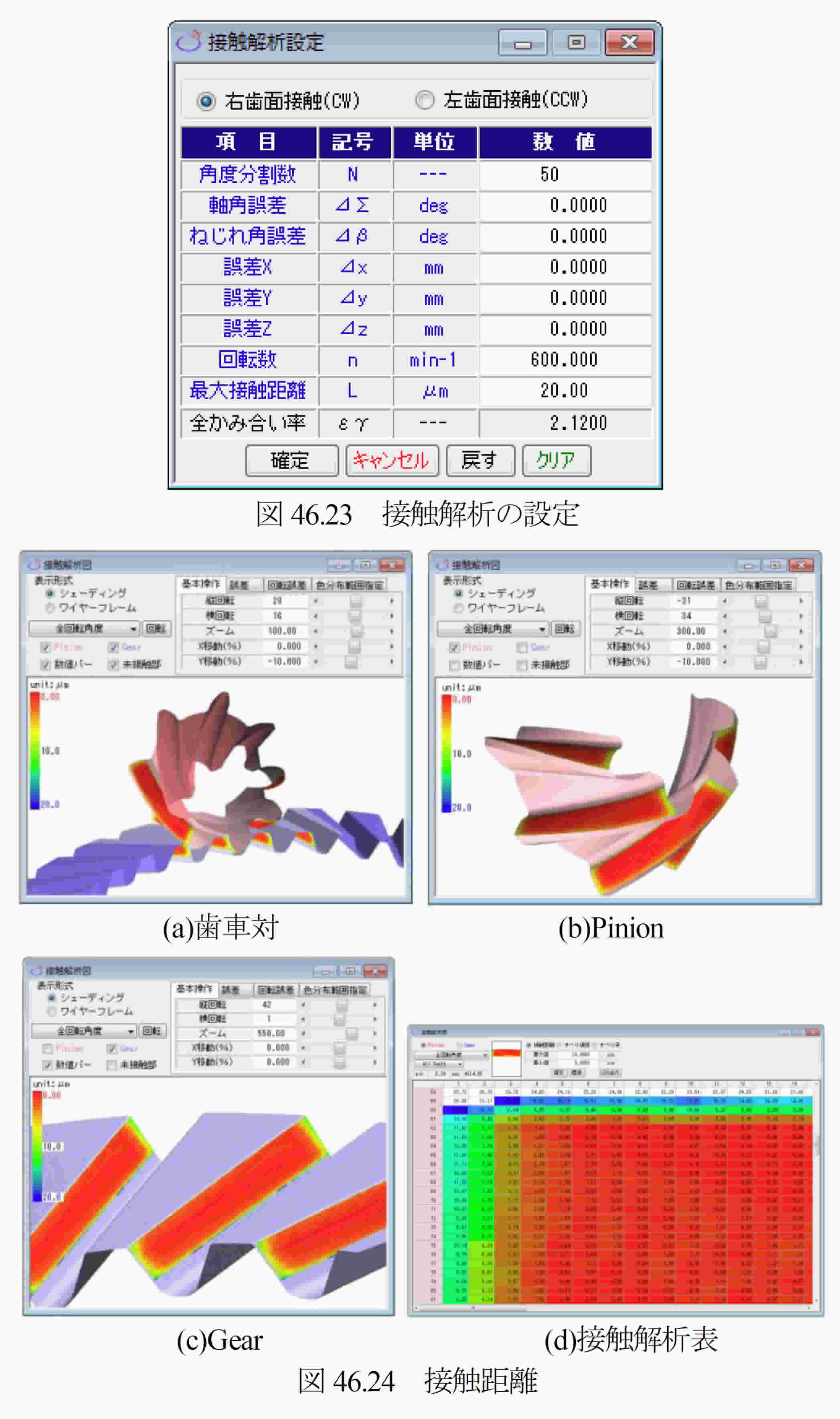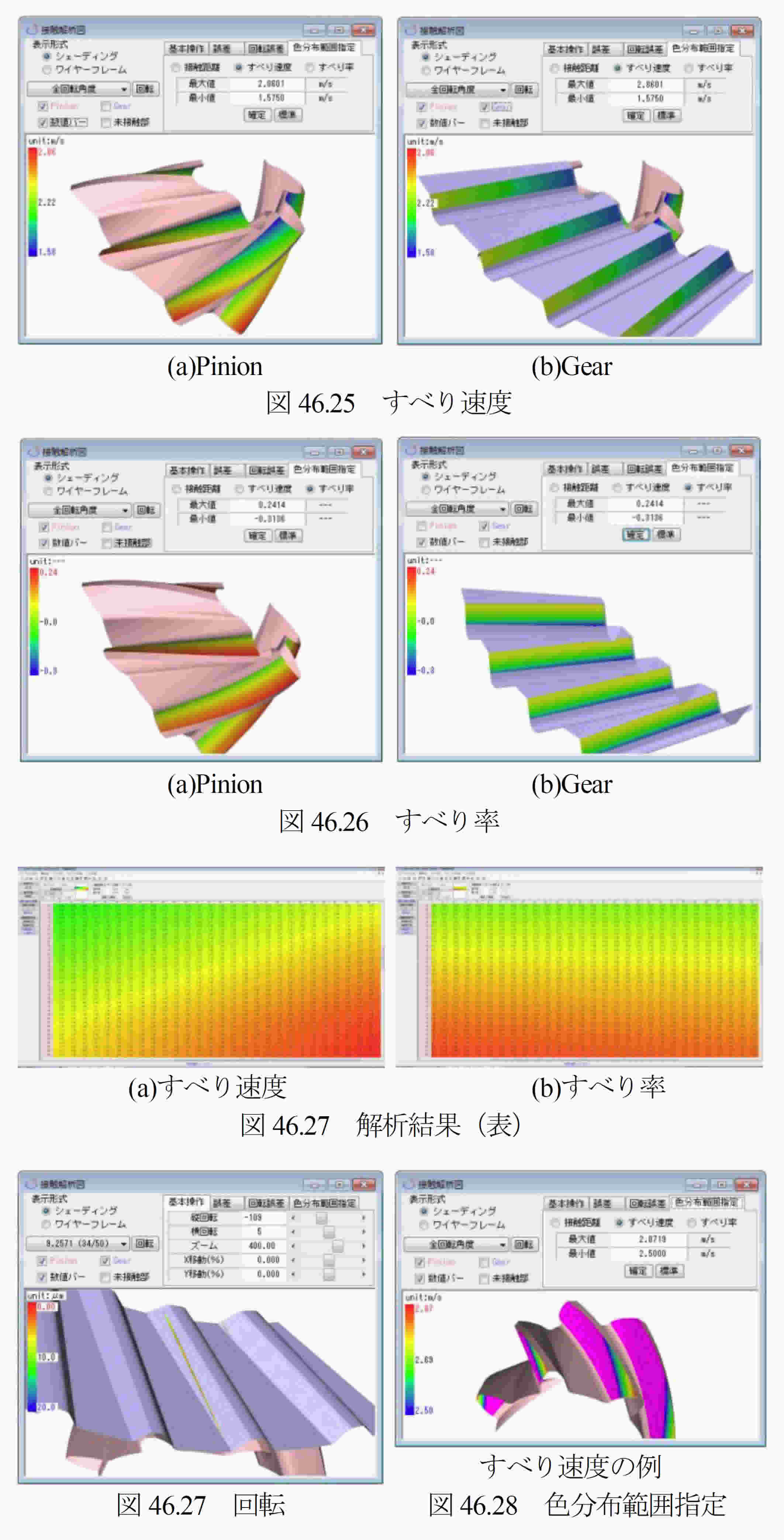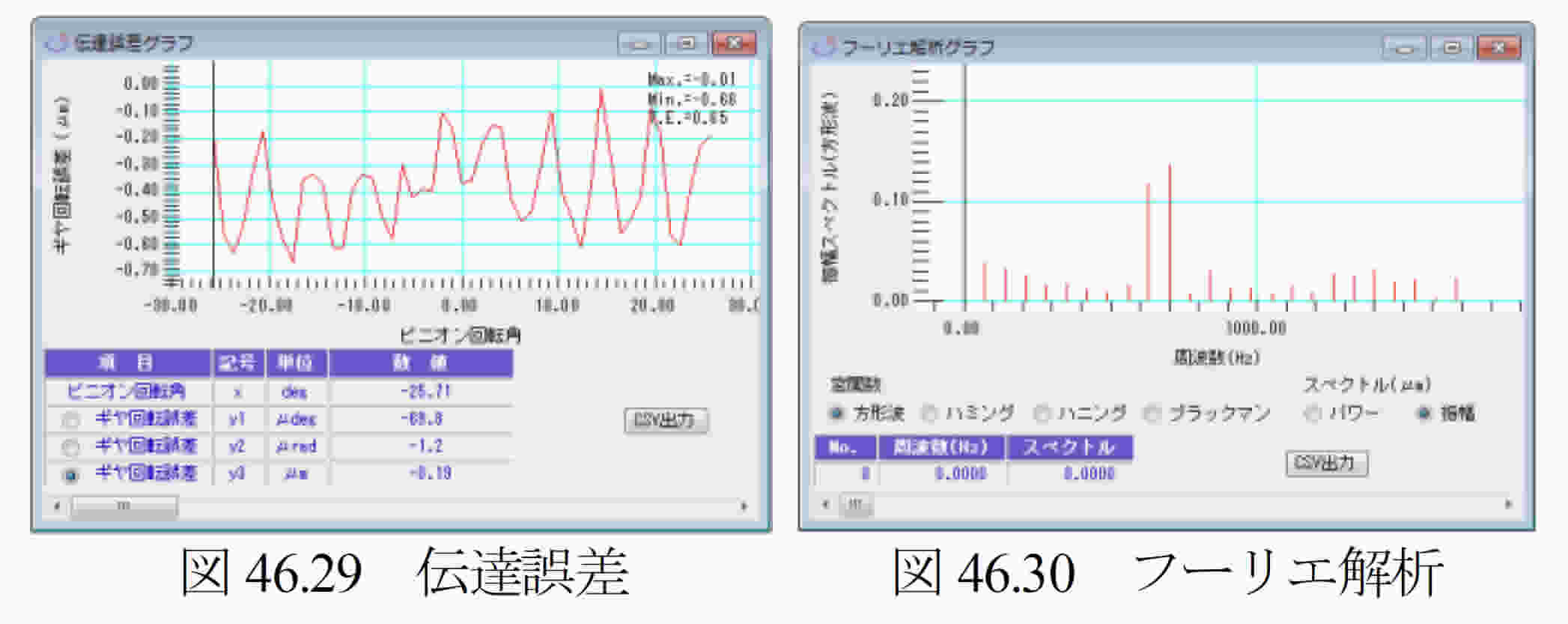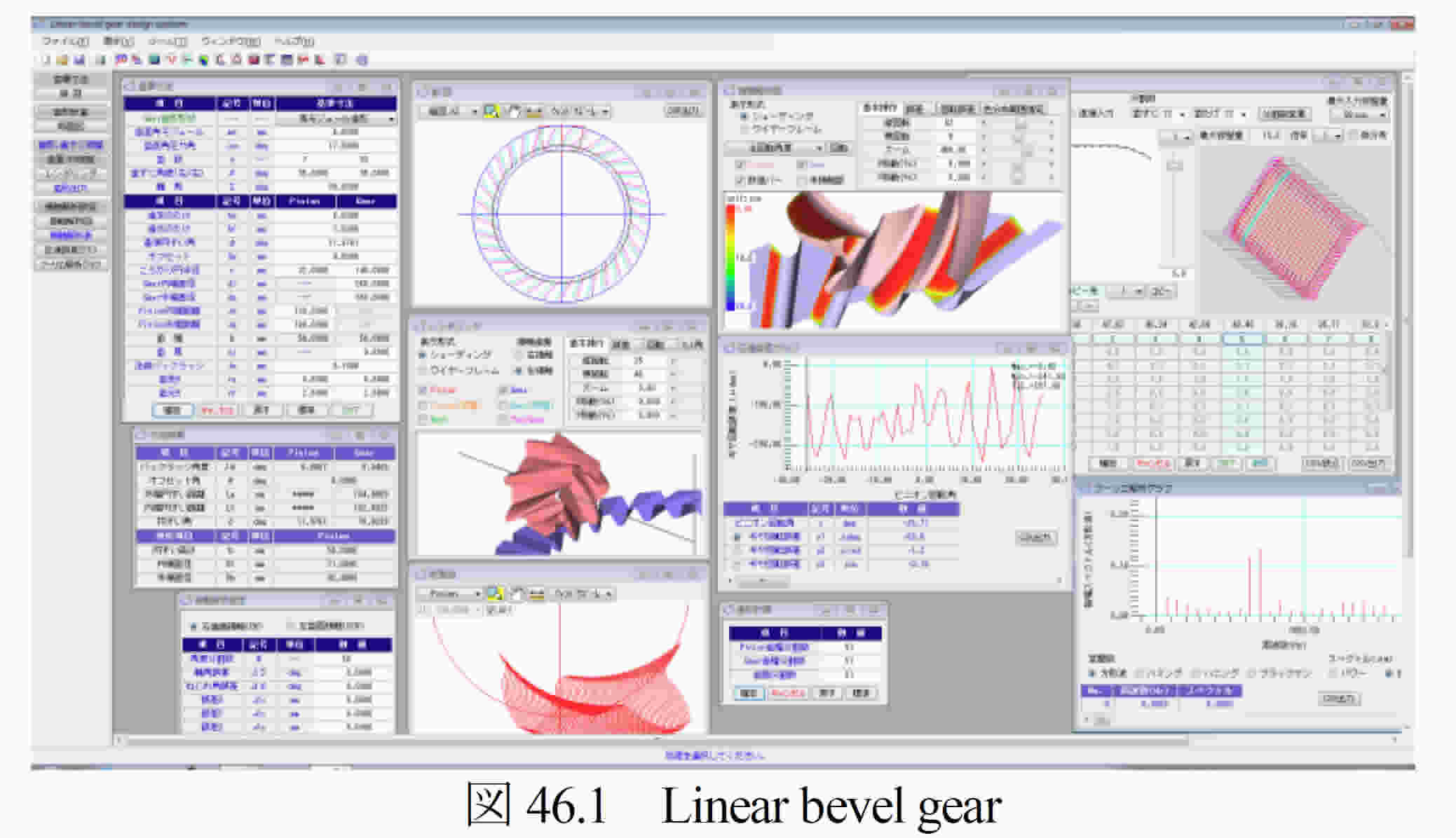
46.1 概要
現在，ベベルギヤはGleason社やKlingelnberg社の専用歯切り盤で加工されていますが，近年，球面インボリュート歯形（カタログ10頁，図2.12参照）を持つベベルギヤをマシニングセンタで加工することも一般化し，小形ベベルギヤの金型や大型ベベルギヤでは目新しいことではなくなってきています．特に大型のベベルギヤでは専用歯切り盤が製造されていないことからマシニングセンタで加工せざるを得ない状況下にあります．
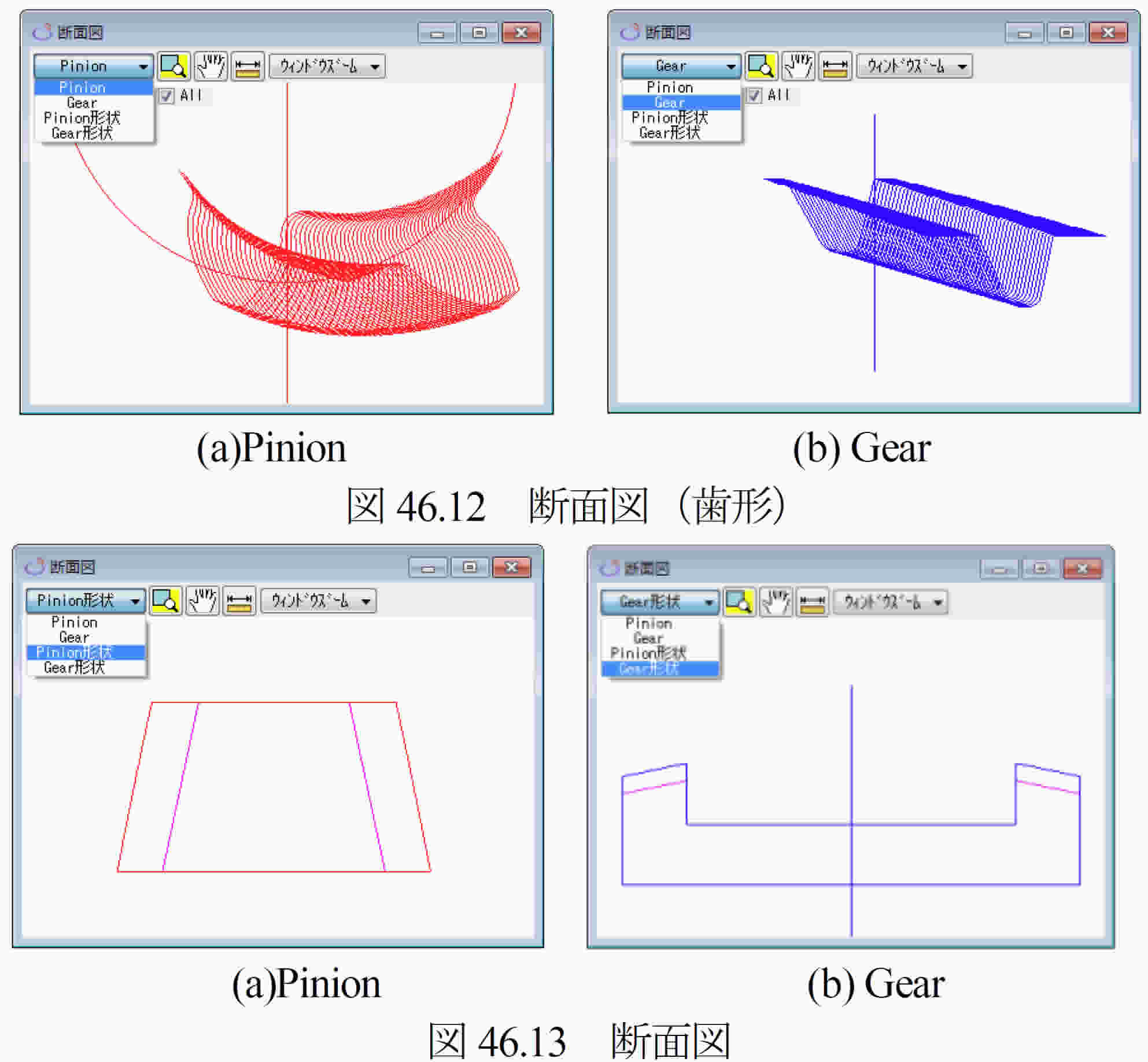
小さな歯車では，工具の摩耗も少なく，ツールパスを細かく運動させることができ，また金型では磨きをすることにより上質な歯面粗さを得ることができます．しかし，大型歯車の場合はエンドミル工具を使用すると工具摩耗や切削（研削）状況などにより，目視観察では問題にならない歯面であっても運転後には図46.2のように歯面に鱗模様が生じてしまいマイクロピッチングが発生する原因となります．このような現象を回避するためには円盤状の砥石で歯面研削しなければなりません．
スパイラルベベルギヤの場合，凸面側歯面は小さな直径を持つ円盤形砥石であれば研削することも可能（隣の歯に接触する可能性がある）ですが，凹面側歯面は研削することができません．
しかし，本ソフトウェアでは，円盤形砥石で歯面研削することができるよう大歯車の歯形と歯すじを直線として，これにかみ合う小歯車の歯形を決定しています（歯面修整も可）．そのため，大歯車の歯面研削はエンドミル形状の工具（スワーフ加工も含む）に比べ大幅な時間短縮が可能です．また，大歯車を内歯ベベルとすること，小歯車にオフセットを与えること，軸角を90°以外とすること，そして，小歯車の歯数を少歯数（1～5歯）とすることができますので大減速で且つ，自由度の高い歯車対を設計することができます．すなわち，このLinear bevel gearは，「設計と加工の多様性」を持つ歯車であると言えます．
Linear bevel gear design systemの構成を表46.1に示します．表中の○は，基本ソフトウェアに含まれ，◎はオプションです．
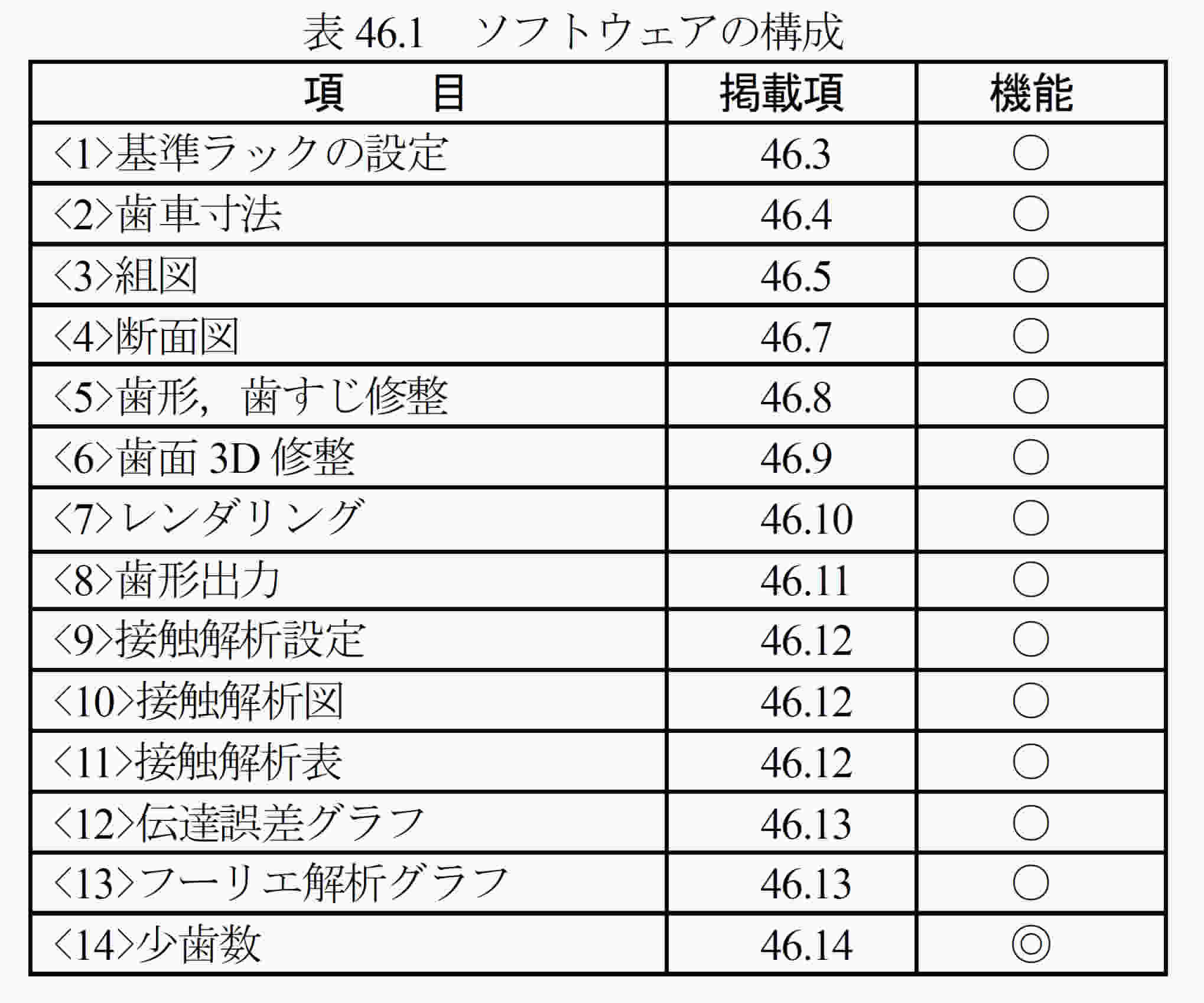
46.3 基準ラックの設定（ツール，プロパティ）
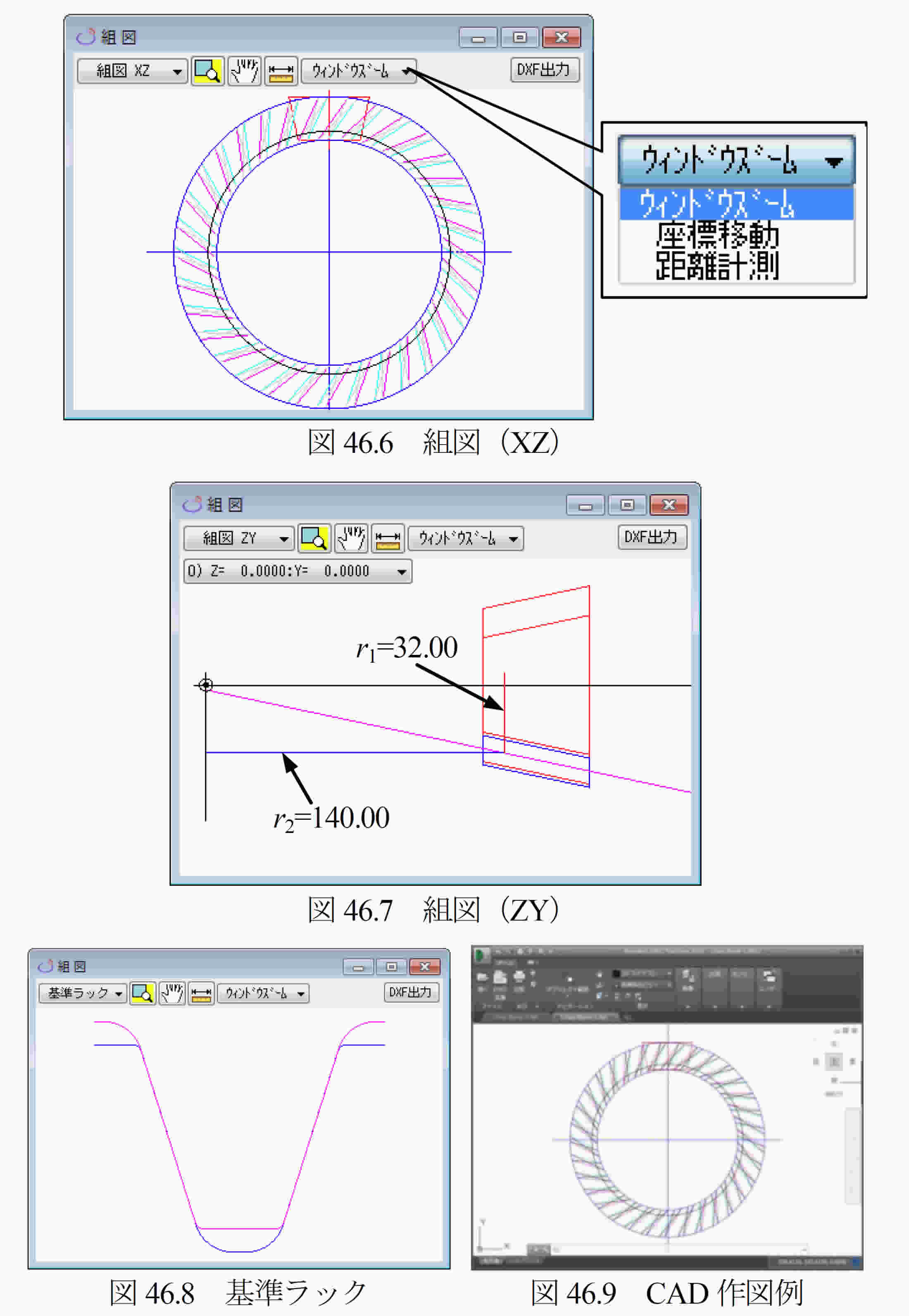
基準ラック（並歯，低歯，特殊）を図46.3で設定し，その基準ラックの形状を表示すことができます．本例では，歯たけを「並歯」とし，圧力角を17.5°とした例を示します．
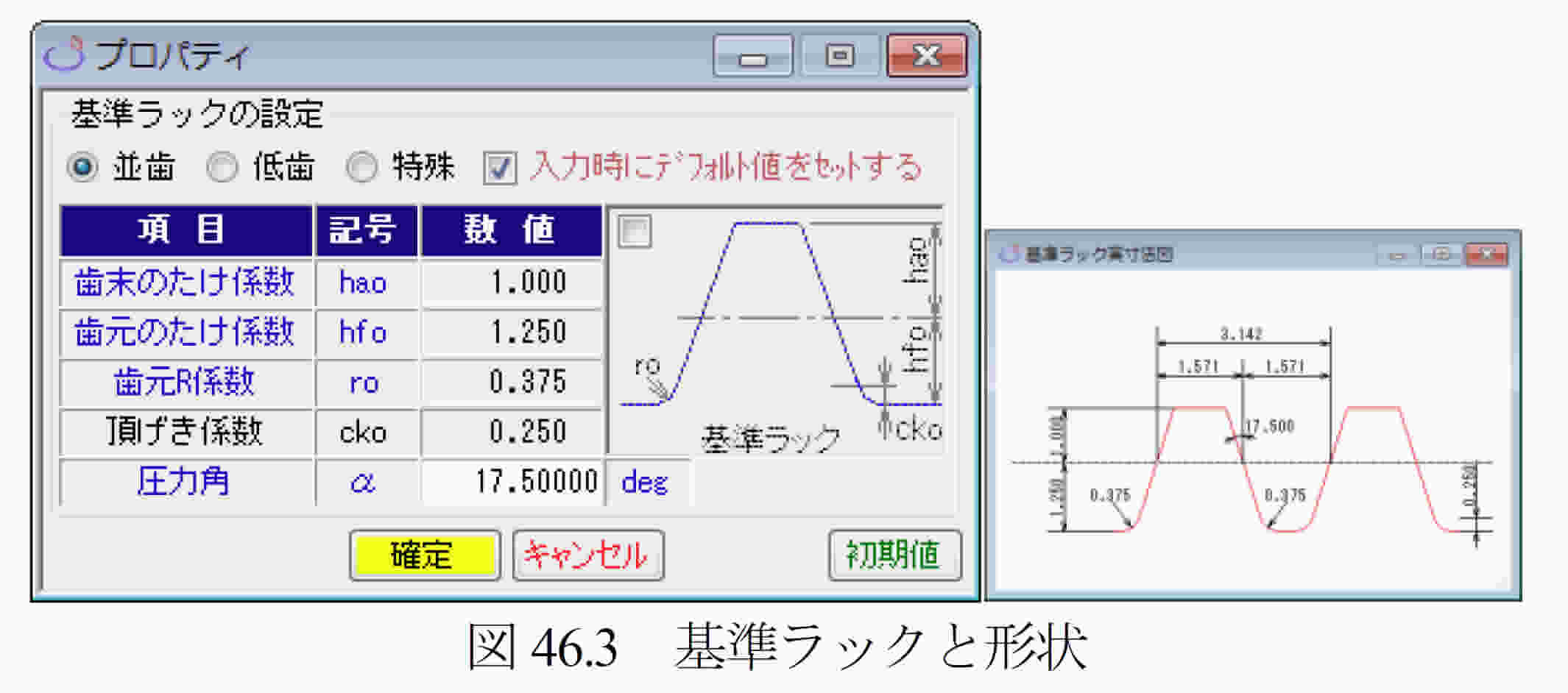
46.4 歯車寸法設定
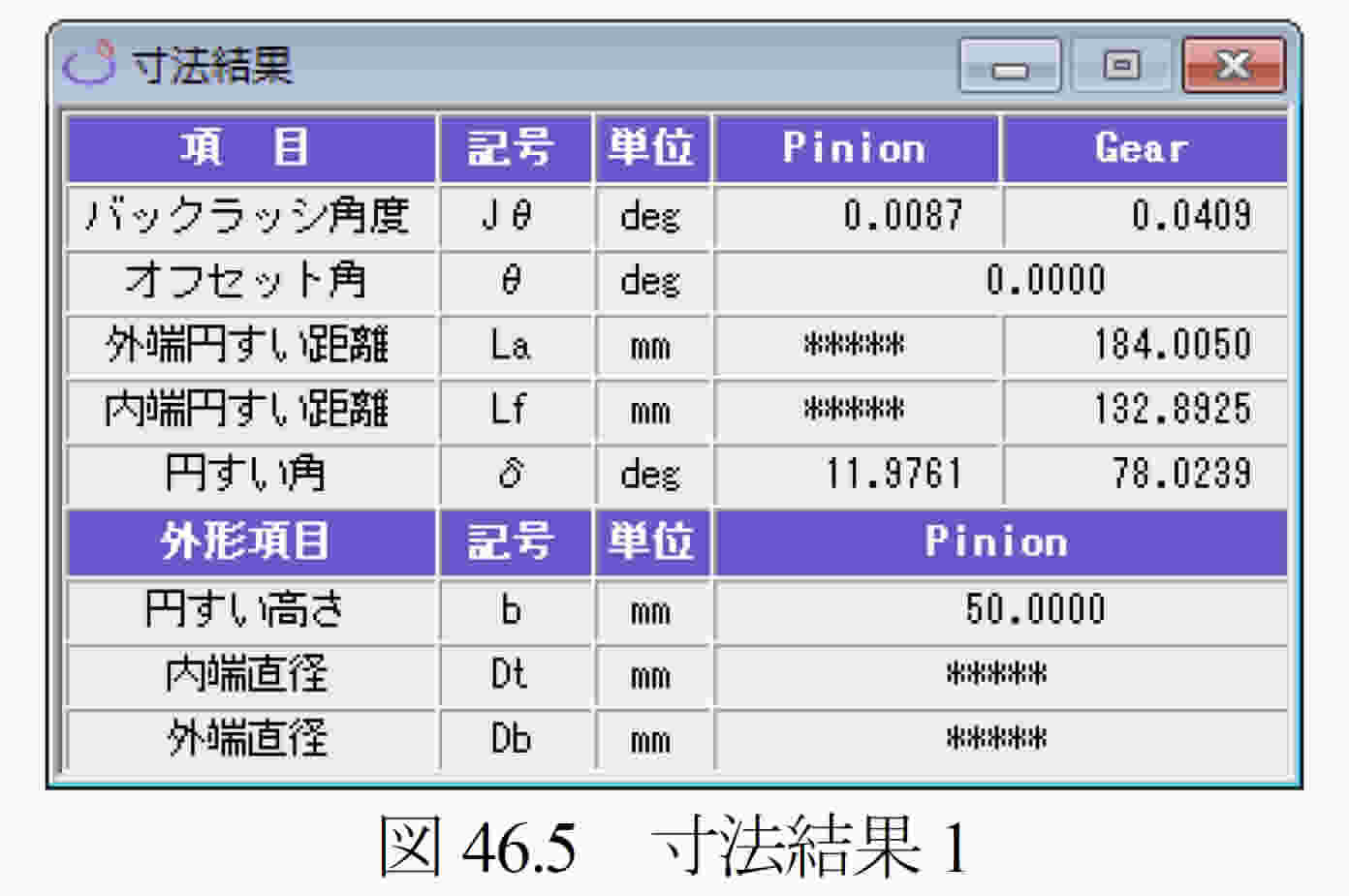
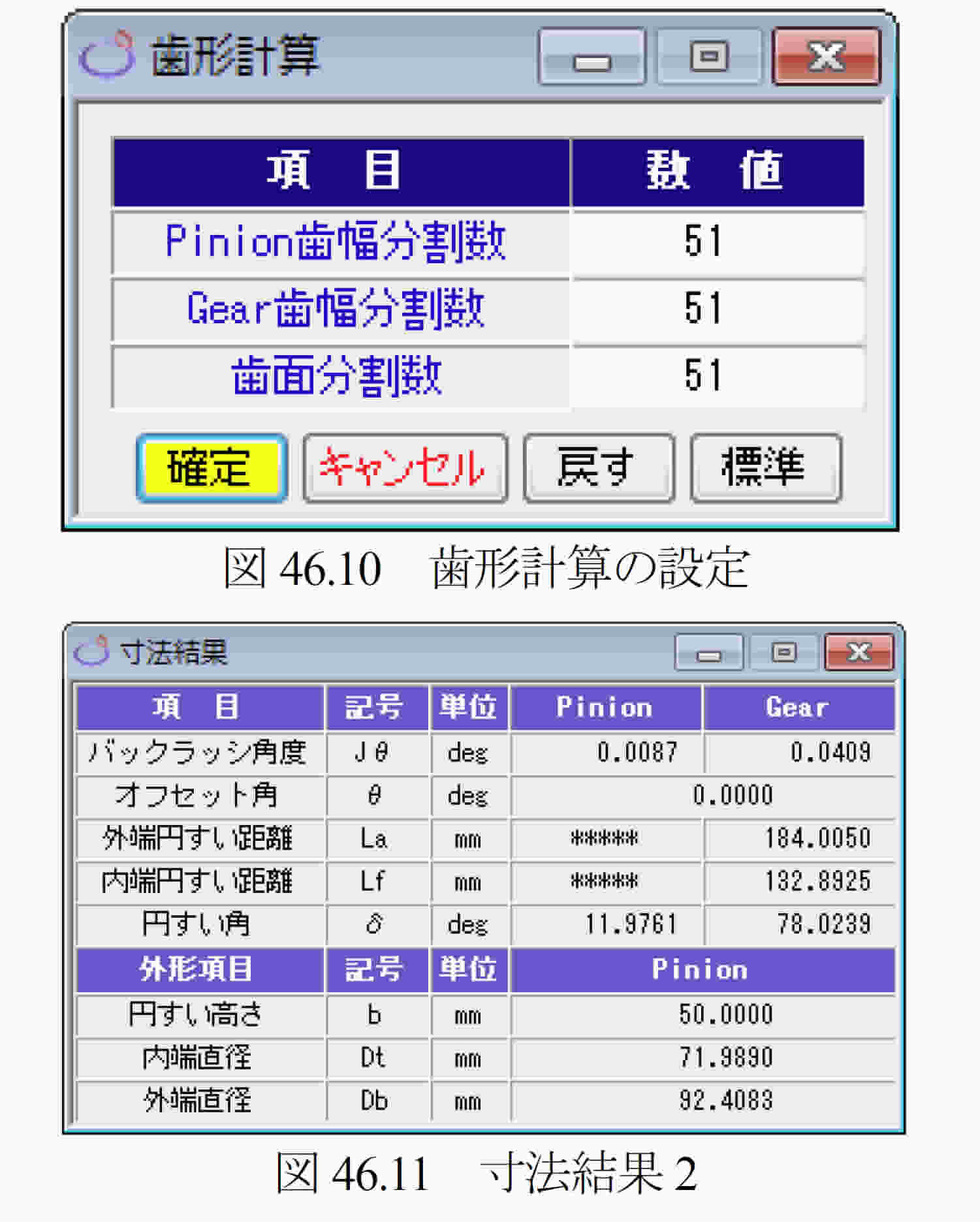
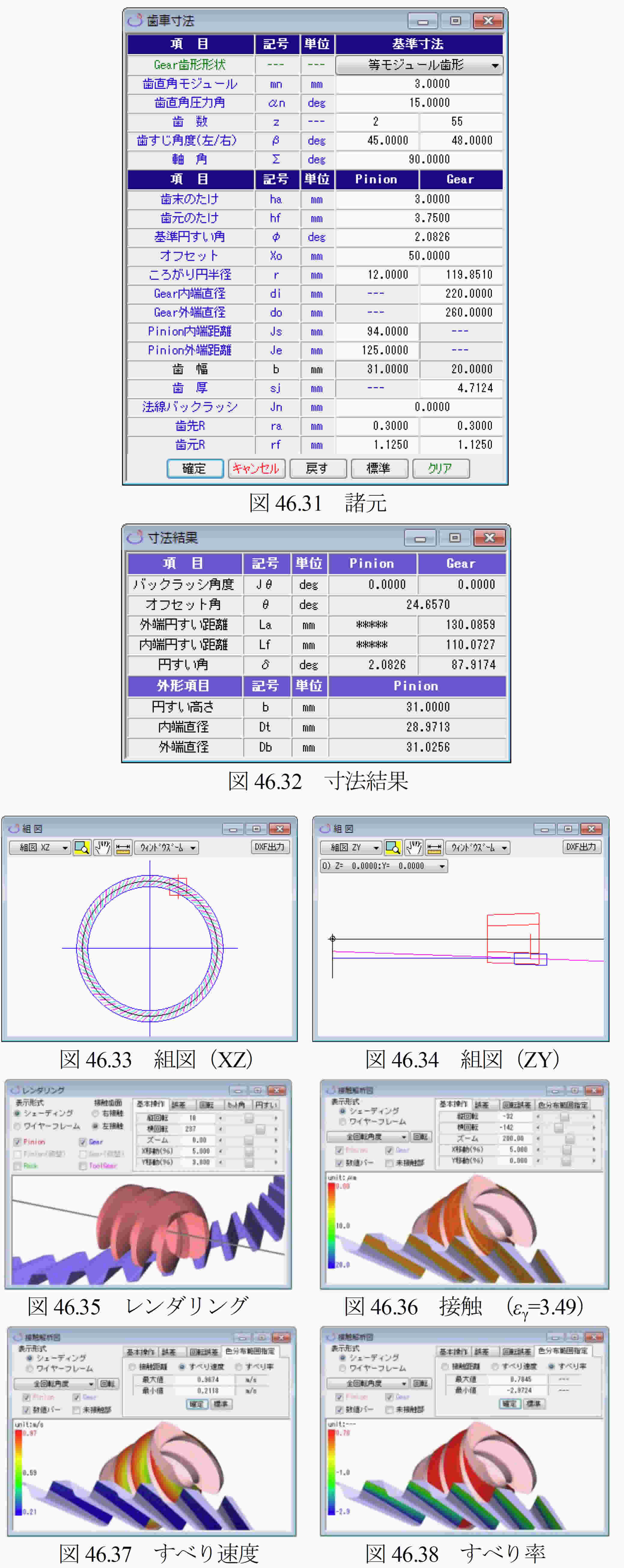
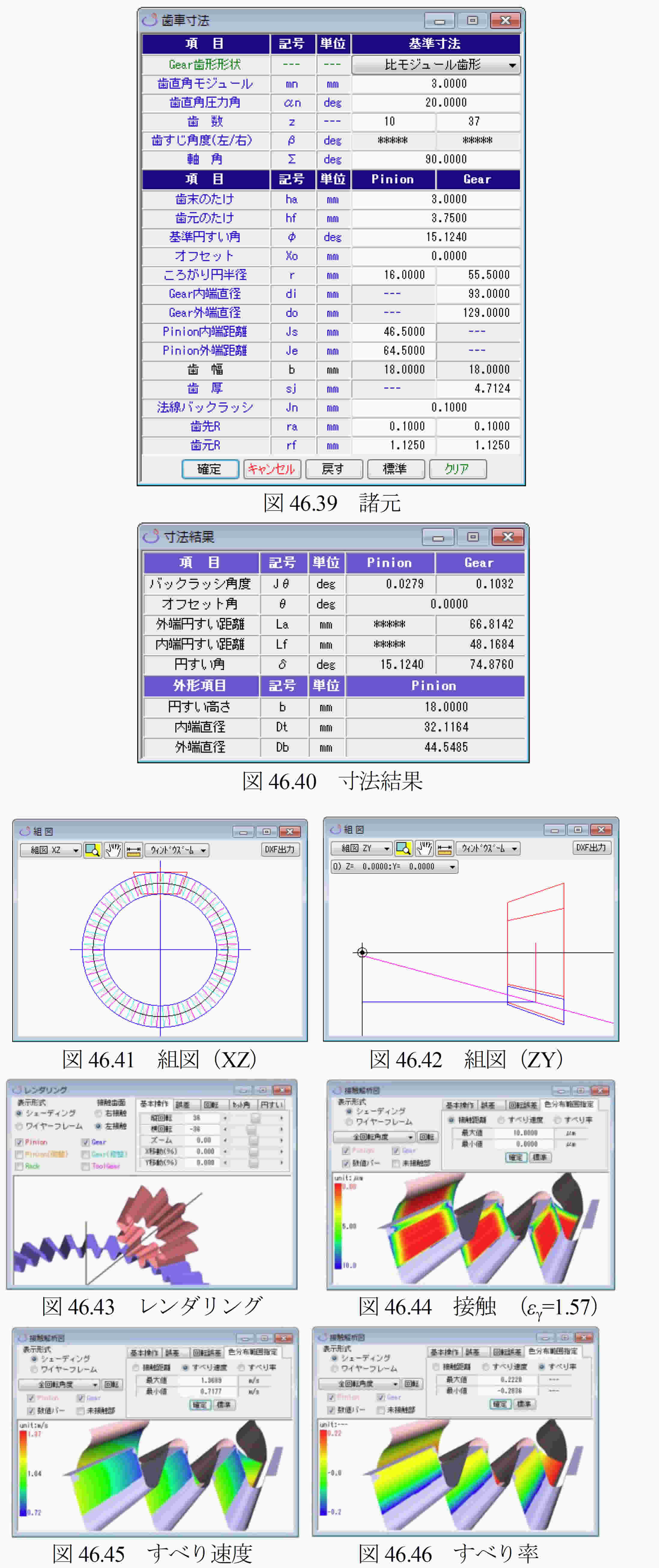
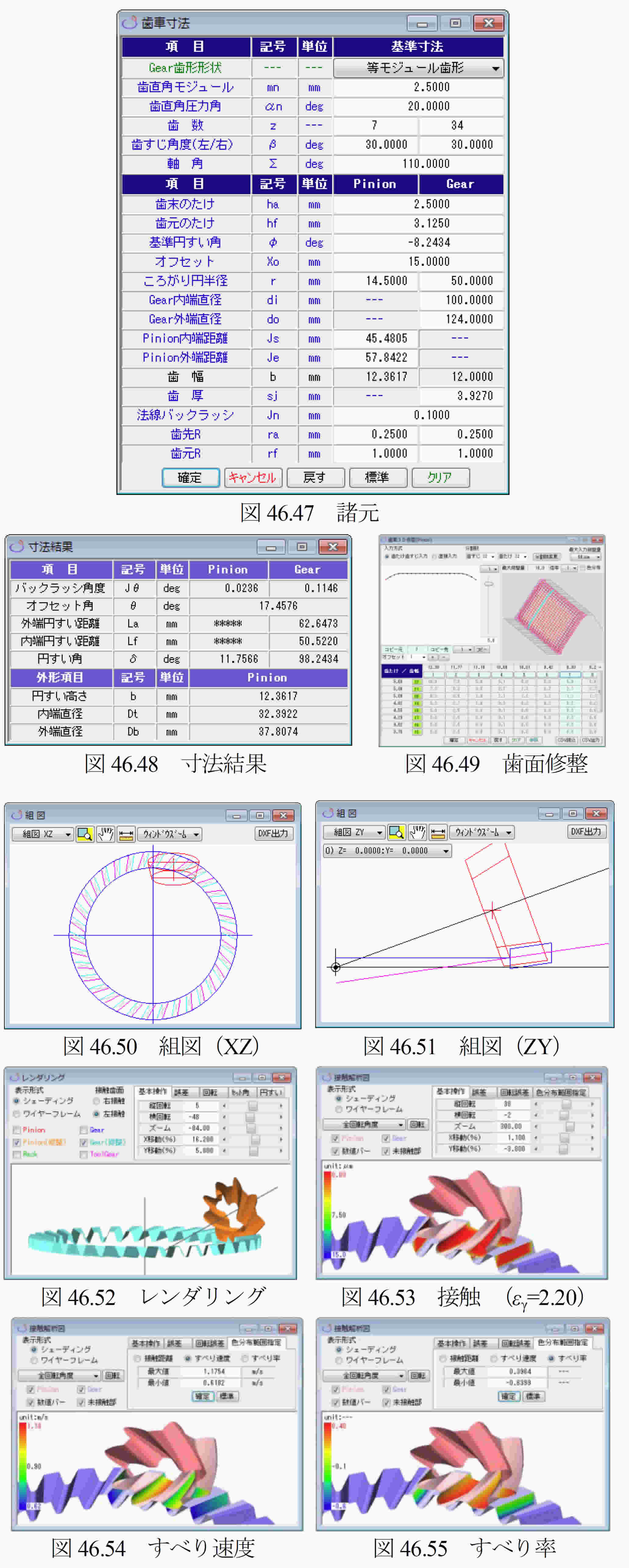
図46.4に諸元入力画面を示します．Gear歯形形状は，「等モジュール歯形」と「比モジュール歯形」の2種類があります．「等モジュール歯形」は，大歯車の歯形を内端部から外端部まで同じモジュールで生成しますが，「比モジュール歯形」（46.15項参照）は，円すい距離に比例するモジュールで歯形を生成します．
AMTEC www.amtecinc.co.jp
で歯面修整量をCSV出力することができ，Excelで作成したデータを
で読み込むことができます．本例では定型の修整を3次元修整に引き継ぎましたが，直接3次元修整値を入力することができます．なお，ギヤは無修整のため省略します．
